
【题目】如图,已知CE⊥AB,垂足为点E,DF⊥AB,垂足为点F,AF=BE,AC=BD,则下列结论:①Rt△AEC≌Rt△BFD;②∠C+∠B=90°;③AC∥BD;④∠A=∠D.
其中正确的结论为____.(填序号)

【答案】①②③
【解析】
由CE⊥AB,DF⊥AB可得△ACE和△BDF都是直角三角形;进而结合AC=BD,可以证明出△ACE≌△BDF;从上面的全等三角形可以得出其中相等的边和角,即可以判断题中正确的选项.
∵CE⊥AB,DF⊥AB
∴△ACE和△BDF都是直角三角形
∵AF=BE,EF公用
∴AE=BF
∵AE=BF,AC=BD,△ACE和△BDF都是直角三角形
∴Rt△AEC≌Rt△BFD
即①正确;
∵Rt△AEC≌Rt△BFD
∴∠CAB=∠ABD
故④错误;
∵在△AEC中,CE⊥AB
∴∠ACE+∠CAB=90°
∵∠ACE+∠CAB=90°,∠CAB=∠ABD
∴∠ACE+∠ABD=90°
故②正确;
∵∠CAB=∠ABD
∴AC∥BD
故③正确.
故答案为:①②③.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】我们在学习“实数”时画了这样一个图,即“以数轴上的单位长为‘1’的线段作一个正方形,然后以原点O为圆心,正方形的对角线长为半径画弧交数轴于点A”,请根据图形回答下列问题:
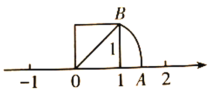
(1)线段OA的长度是多少?(要求写出求解过程)
(2)这个图形的目的是为了说明什么?
(3)这种研究和解决问题的方式体现了 的数学思想方法.(将下列符合的选项序号填在横线上)
A.数形结合 B.代入 C.换元 D.归纳
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.
(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=2,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
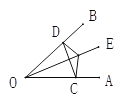
【题目】如图,点E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别为C、D.
求证:(1)∠ECD=∠EDC;
(2)OC=OD;
(3)OE是线段CD的垂直平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是反比例函数y=![]() 的图象的一个分支,对于给出的下列说法:
的图象的一个分支,对于给出的下列说法:

①常数k的取值范围k>2;②另一分支在第三象限;③在函数图象上取点A(a1,b1)和点B(a2,b2),当a1>a2时,则b1<b2;④在函数图象的某一分支上取点A(a1,b1)和点B(a2,b2),当a1>a2时,则b1<b2.其中正确的是__________.(在横线上填上正确的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线相交于点O,AE平分∠BAD交BC于E, 若∠CAE=15°则∠BOE=( )

A. 30° B. 45° C. 60° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光明中学全体学生900人参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,结合图中所给信息解答下列问题:
![]() 填写下表:
填写下表:
中位数 | 众数 | |
随机抽取的50人的社会实践活动成绩 |
![]() 估计光明中学全体学生社会实践活动成绩的总分.
估计光明中学全体学生社会实践活动成绩的总分.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com