
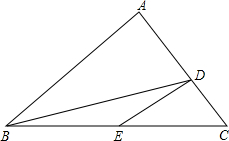
 如图,在△ABC中,D、E分别是AC、BC边上的一点,AD=2DC,BE=EC,若△DBE的面积为1,则△ABC的面积等于( )
如图,在△ABC中,D、E分别是AC、BC边上的一点,AD=2DC,BE=EC,若△DBE的面积为1,则△ABC的面积等于( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
分析 如图,作辅助线;首先证明AM=3DN,此为解题的关键性结论;运用运用三角形的面积公式,即可解决问题.
解答 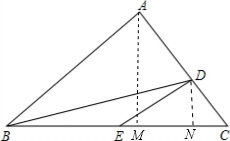 解:如图,过点A作AM⊥BC,过点D作DN⊥BC;
解:如图,过点A作AM⊥BC,过点D作DN⊥BC;
则AM∥DN;
∴△AMC∽△DNC,
∴$\frac{AM}{DN}=\frac{AC}{DC}$,而AD=2DC,
∴AM=3DN(设DN为λ);设BE=EC=μ,
∴$\frac{{S}_{△ABC}}{{S}_{△BED}}=\frac{\frac{1}{2}×2μ•3λ}{\frac{1}{2}×μ•λ}$=6,而S△BED=1,
∴S△ABC=6,
故选B.
点评 该题主要考查了三角形的面积公式、相似三角形的判定及其性质等几何知识点及其应用问题;解题的关键是作辅助线,灵活运用三角形的面积公式来分析、判断、解答.


 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:解答题
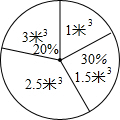 为了宣传保护水源、节约用水的生活方式,某同学利用课余时间对某小区居民的用水情况进行了统计,并将今年1月居民的节水量统计整理成如下统计图表:
为了宣传保护水源、节约用水的生活方式,某同学利用课余时间对某小区居民的用水情况进行了统计,并将今年1月居民的节水量统计整理成如下统计图表:| 节水量(米3) | 1 | 1.5 | 2.5 | 3 |
| 户数 | a | 90 | 100 | b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
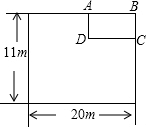 某单位为响应政府发出的全民健身的号召,打算在长和宽分别为20m和11m的长方形大厅内修建一个长方形健身房ABCD.该健身房的四面墙壁中有两侧沿用大厅的旧墙壁(如图为平面示意图),已知装修旧墙壁的费用为a元/m2,比新建(含装修)墙壁的费用每平方米少50元.设健身房的高为3m,一面旧墙壁AB的长为xm,BC为(x-5)米,修建健身房墙壁的总投入为多少元?(用含a,x的代数式表示)
某单位为响应政府发出的全民健身的号召,打算在长和宽分别为20m和11m的长方形大厅内修建一个长方形健身房ABCD.该健身房的四面墙壁中有两侧沿用大厅的旧墙壁(如图为平面示意图),已知装修旧墙壁的费用为a元/m2,比新建(含装修)墙壁的费用每平方米少50元.设健身房的高为3m,一面旧墙壁AB的长为xm,BC为(x-5)米,修建健身房墙壁的总投入为多少元?(用含a,x的代数式表示)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com