
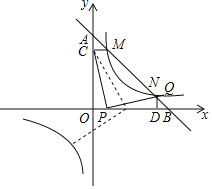
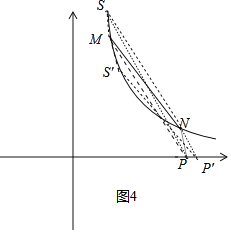
【题目】如图,一次函数y=﹣x+5的图象与坐标轴交于A,B两点,与反比例函数y=![]() 的图象交于M,N两点,过点M作MC⊥y轴于点C,且CM=1,过点N作ND⊥x轴于点D,且DN=1.已知点P是x轴(除原点O外)上一点.
的图象交于M,N两点,过点M作MC⊥y轴于点C,且CM=1,过点N作ND⊥x轴于点D,且DN=1.已知点P是x轴(除原点O外)上一点.
(1)直接写出M、N的坐标及k的值;
(2)将线段CP绕点P按顺时针或逆时针旋转90°得到线段PQ,当点P滑动时,点Q能否在反比例函数的图象上?如果能,求出所有的点Q的坐标;如果不能,请说明理由;
(3)当点P滑动时,是否存在反比例函数图象(第一象限的一支)上的点S,使得以P、S、M、N四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点S的坐标;若不存在,请说明理由.
【答案】(1)M(1,4),N(4,1),k=4;(2)(2+2![]() ,﹣2+2
,﹣2+2![]() )或(2﹣2
)或(2﹣2![]() ,﹣2﹣2
,﹣2﹣2![]() )或(﹣2,﹣2);(3)(
)或(﹣2,﹣2);(3)(![]() ,5)或(
,5)或(![]() ,3).
,3).
【解析】
(1)利用待定系数法即可解决问题;
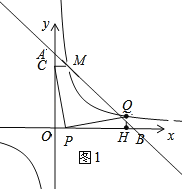
(2)分三种情形求解:①如图2,点P在x轴的正半轴上时,绕P顺时针旋转到点Q,根据△COP≌△PHQ,得CO=PH,OP=QH,设P(x,0),表示Q(x+4,x),代入反比例函数的关系式中可得Q的两个坐标;②如图3,点P在x轴的负半轴上时;③如图4,点P在x轴的正半轴上时,绕P逆时针旋转到点Q,同理可得结论.
(3)分两种情形分别求解即可;
解:(1)由题意M(1,4),n(4,1),
∵点M在y=![]() 上,
上,
∴k=4;
(2)当点P滑动时,点Q能在反比例函数的图象上;
如图1,CP=PQ,∠CPQ=90°,
过Q作QH⊥x轴于H,
易得:△COP≌△PHQ,
∴CO=PH,OP=QH,
由(2)知:反比例函数的解析式:y=![]() ;
;
当x=1时,y=4,
∴M(1,4),
∴OC=PH=4
设P(x,0),
∴Q(x+4,x),
当点Q落在反比例函数的图象上时,
x(x+4)=4,
x2+4x+4=8,
x=﹣2±![]() ,
,
当x=﹣2±![]() 时,x+4=2+
时,x+4=2+![]() ,如图1,Q(2+2
,如图1,Q(2+2![]() ,2+2
,2+2![]() );
);
当x=﹣2﹣2![]() 时,x+4=2﹣2
时,x+4=2﹣2![]() ,如图2,Q(2﹣2
,如图2,Q(2﹣2![]() ,2﹣2
,2﹣2![]() );
);
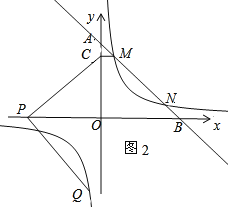
如图3,CP=PQ,∠CPQ=90°,设P(x,0)
过P作GH∥y轴,过C作CG⊥GH,过Q作QH⊥GH,
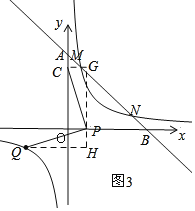
易得:△CPG≌△PQH,
∴PG=QH=4,CG=PH=x,
∴Q(x﹣4,﹣x),
同理得:﹣x(x﹣4)=4,
解得:x1=x2=2,
∴Q(﹣2,﹣2),
综上所述,点Q的坐标为(2+2![]() ,﹣2+2
,﹣2+2![]() )或(2﹣2
)或(2﹣2![]() ,﹣2﹣2
,﹣2﹣2![]() )或(﹣2,﹣2).
)或(﹣2,﹣2).
(3)当MN为平行四边形的对角线时,根据MN的中点的纵坐标为![]() ,可得点S的纵坐标为5,即S(
,可得点S的纵坐标为5,即S(![]() ,5);
,5);
当MN为平行四边形的边时,易知点S的纵坐标为3,即S(![]() ,3);
,3);
综上所述,满足条件的点S的坐标为(![]() ,5)或(
,5)或(![]() ,3).
,3).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
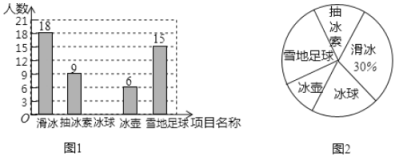
【题目】哈尔滨市教育局以冰雪节为契机,在全市校园内开展多姿多彩的冰雪活动.某校为激发学生参与冰雪体育活动热情,开设了“滑冰、抽冰尜、冰球、冰壶、雪地足球”五个冰雪项目,并开展了以“我最喜欢的冰雪项目”为主题的调查活动,围绕“在滑冰、抽冰尜、冰球、冰壶、雪地足球中,你最喜欢的冰雪项目是什么?(每名学生必选且只选一个)”的问题在全校范围内随机抽取了部分学生进行问卷调查,根据调查结果绘制了如图所示的不完整的统计图.请根据统计图的信息回答下列问题:
(1)本次调查共抽取了多少名学生?
(2)求本次调查中,最喜欢冰球项目的人数,并补全条形统计图;
(3)若该中学共有1800名学生,请你估计该中学最喜欢雪地足球的学生约有多少名.
查看答案和解析>>
科目:初中数学 来源: 题型:
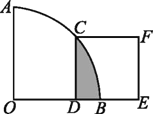
【题目】如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是![]() 的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2
的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2![]() 时,阴影部分的面积为________
时,阴影部分的面积为________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=4,BC=3,点D为边AB的中点.点P从点A出发,沿AC方向以每秒1个单位长度的速度向终点C运动,同时点Q从点C出发,以每秒2个单位长度的速度先沿CB方向运动到点B,再沿BA方向向终点A运动,以DP、DQ为邻边构造PEQD,设点P运动的时间为t秒.
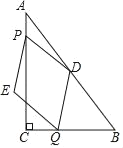
(1)设点Q到边AC的距离为h,直接用含t的代数式表示h;
(2)当点E落在AC边上时,求t的值;
(3)当点Q在边AB上时,设PEQD的面积为S(S>0),求S与t之间的函数关系式;
(4)连接CD,直接写出CD将PEQD分成的两部分图形面积相等时t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市民广场有一个直径16米的圆形喷水池,喷水池的周边有一圈喷水头(喷水头高度忽略不计),各方向喷出的水柱恰好在喷水池中心的装饰物OA的顶端A处汇合,水柱离中心3米处达最高5米,如图所示建立直角坐标系.王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的他站立时必须在离水池中心O________米以内.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,抛物线![]() 经过点A(-2,0),B(4,0)两点,与
经过点A(-2,0),B(4,0)两点,与![]() 轴交于点C,点D是抛物线上一个动点,设点D的横坐标为
轴交于点C,点D是抛物线上一个动点,设点D的横坐标为![]() .连接AC,BC,DB,DC,
.连接AC,BC,DB,DC,
(1)求抛物线的函数表达式;
(2)△BCD的面积等于△AOC的面积的![]() 时,求
时,求![]() 的值;
的值;
(3)在(2)的条件下,若点M是![]() 轴上的一个动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.
轴上的一个动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
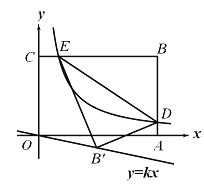
【题目】如图,平面直角坐标系![]() 中,矩形
中,矩形![]() 的边
的边![]() 、
、![]() 分别落在
分别落在![]() 、
、![]() 轴上,点
轴上,点![]() 坐标为
坐标为![]() ,反比例函数
,反比例函数![]() 的图象与
的图象与![]() 边交于点
边交于点![]() ,与
,与![]() 边交于点
边交于点![]() ,连结
,连结![]() ,将
,将![]() 沿
沿![]() 翻折至
翻折至![]() 处,点
处,点![]() 恰好落在正比例函数
恰好落在正比例函数![]() 图象上,则
图象上,则![]() 的值是
的值是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近几年购物的支付方式日益增多,某数学兴趣小组就此进行了抽样调查,调查结果显示支付方式有:![]() 微信、
微信、![]() 支付宝、
支付宝、![]() 现金、
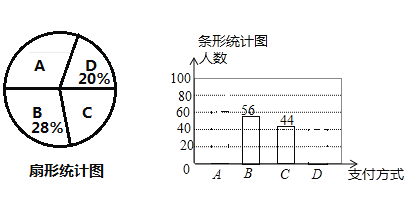
现金、![]() 其他.该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:
其他.该小组对某超市一天内购买者的支付方式进行调查统计,得到如下两幅不完整的统计图.请你根据统计图提供的信息,解答下列问题:
(1)本次一共调查了 名购买者?
(2)请补全条形统计图;在扇形统计图中,![]() 种支付方式所对应的圆心角为 度;
种支付方式所对应的圆心角为 度;
(3)若该超市这一周内有2000名购买者,请你估计使用![]() 和
和![]() 两种支付方式的购买者共有多少名?
两种支付方式的购买者共有多少名?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com