
����Ŀ��ɽ����ɽ���й���ʷ�Ļ���ɽ������ʱ�ڽ���������Яĸ�����ڴ˱��ٶ����ƣ���ͼ1������ɽ�Ͻ�����ĸ�ӵ�����ij�οͼƻ�������������ĸ߶ȣ������ο���ֱ�ӵ�������ײ�����˸��οͼƻ���������߶�����������ĸ߶ȣ���ͼ2����������ɽ���½�A���������ͷ��C������Ϊ75�㣬����A������������10����P��ʱ���������ͷ��C�����Ǹպ�Ϊ45�㣬��֪ɽ�µ��¶�i=1��3����O��A��B��ͬһֱ���ϣ�������ĸ߶ȣ����������߶Ⱥ��Բ��ƣ������ȷ��0.1�ף��ο����ݣ�cos75���0.3��tan75���3.7��![]() ��1.4��
��1.4��![]() ��1.7��
��1.7��![]() ��3.2��
��3.2��
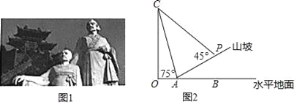
���𰸡�17.5
��������
����P��PE��OB�ڵ�E��PF��OC�ڵ�F����PE=x����AE=3x����Rt��AEP�и��ݹ��ɶ����ɵ�PE=![]() ����AE=3
����AE=3![]() ����CF=PF=m�ף���OC=��m+
����CF=PF=m�ף���OC=��m+![]() ���ס�OA��m-3
���ס�OA��m-3![]() ���ף���Rt��AOC�У���tan75��=
���ף���Rt��AOC�У���tan75��=![]() ���m��ֵ���̶��ɵô𰸣�
���m��ֵ���̶��ɵô𰸣�
�⣺����P��PE��OB�ڵ�E��PF��OC�ڵ�F��
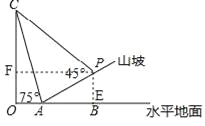

��i=1��3��AP=10��
��PE=x����AE=3x��
��Rt��AEP��x2+��3x��2=102��
��ã�x=![]() ��x=��
��x=��![]() ���ᣩ��
���ᣩ��
��PE=![]() ����AE=3
����AE=3![]() ��
��
�ߡ�CPF=��PCF=45����
��CF=PF��
��CF=PF=m�ף���OC=��m+![]() ���ף�OA=��m��3
���ף�OA=��m��3![]() ���ף�
���ף�
��Rt��AOC��tan75��=![]() =
=![]() ����m+
����m+![]() =tan75����m��3
=tan75����m��3![]() ����
����
��ã�m��14.3��
��OC=14.3+![]() ��17.5�ף�
��17.5�ף�
������ĸ߶�ԼΪ17.5�ף�


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������֪�����졢Ӧ�������������о�һ�ּ���ģ�ͣ�
����֪��
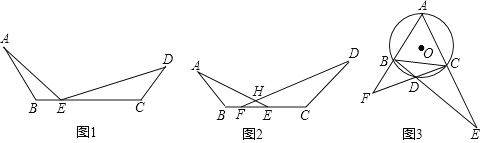
��ͼ1����֪��E���߶�BC��һ�㣬��![]() ��֤��
��֤��![]() ��
��![]() ��
��
�����죩
��ͼ2����֪��E��F���߶�BC�����㣬AE��DF���ڵ�H����![]() ��֤��
��֤��![]() ��
��![]() ��
��
��Ӧ�ã�
��ͼ3��![]() �ǵȱ�
�ǵȱ�![]() �����Բ����D��
�����Բ����D��![]() ��һ�㣬����BD���ӳ���AC���ӳ����ڵ�E������CD���ӳ���AB���ӳ����ڵ�
��һ�㣬����BD���ӳ���AC���ӳ����ڵ�E������CD���ӳ���AB���ӳ����ڵ�![]() ����BF��BC��CE���߶εĹ�ϵ����˵�����ɣ�
����BF��BC��CE���߶εĹ�ϵ����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
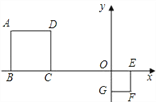
����Ŀ��������ABCD��������OEFG�У���D�͵�F������ֱ�Ϊ����3��2���ͣ�1����1�����������������ε�λ�����ĵ�����Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
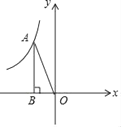
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����������y����![]() �ڵڶ�����ͼ������һ��A������A��AB��x���ڵ�B����S��AOB��_____��
�ڵڶ�����ͼ������һ��A������A��AB��x���ڵ�B����S��AOB��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����45���ǵ����ǰ��ֱ�Ƕ������һ�ſ�Ϊ3cm��ֽ�������ϣ���һ����
����ֽ������һ�����ϣ�������ǰ��һ����ֽ����һ�����ڵ�ֱ�߳�30���ǣ���ͼ��3����
�����ǰ�����ߵij�Ϊ�� ��
A. ![]() B.
B. ![]() C.
C.![]()
![]() D.
D. ![]()
![]()

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ڽ��ڡ�O����I����ABC�����ģ���AIC=124������E��AD���ӳ����ϣ����CDE�Ķ���Ϊ��������
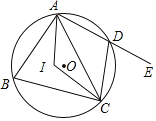
A. 56�� B. 62�� C. 68�� D. 78��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB�ǡ�O��ֱ����P��BA�ӳ�����һ�㣬PC�С�O�ڵ�C��CG�ǡ�O���ң�CG��AB������ΪD��
��1����֤����PCA=��ABC��
��2������A��AE��PC����O�ڵ�E����CD�ڵ�F������BE����cos��P=![]() ��CF=10����BE�ij�
��CF=10����BE�ij�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y����![]() x��
x��![]() �ֱ���x�ᡢy�ύ��B��C���㣬��A��x���ϣ���ACB��90��,������
�ֱ���x�ᡢy�ύ��B��C���㣬��A��x���ϣ���ACB��90��,������![]() ��ax2��bx��
��ax2��bx��![]() ����A��B���㣮
����A��B���㣮
��1����A��B��������ꣻ
��2���������ߵĽ���ʽ��
��3����M��ֱ��BC�Ϸ��������ϵ�һ�㣬����M����MH��BC�ڵ�H������MD��y�ύBC�ڵ�D����![]() DMH�ܳ������ֵ��
DMH�ܳ������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
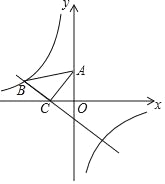
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���һ�����ֱ�����ǰ�ABC���ڵڶ����ޣ�б�������������ϣ���C����Ϊ(��1��0)����A������Ϊ(0��2)��һ�κ���y��kx+b��ͼ����B��C������������y��![]() ��ͼ��Ҳ������B��
��ͼ��Ҳ������B��
(1)���������Ĺ�ϵʽ��
(2)ֱ��д����x��0ʱ��kx+b��![]() ��0�Ľ⼯��
��0�Ľ⼯��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com