
【题目】如图,在△ABC中,AB=AC,∠ABC=72°. 
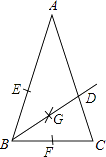
(1)用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹,不要求写作法);
(2)在(1)中作出∠ABC的平分线BD后,求∠BDC的度数.
【答案】
(1)解:①一点B为圆心,以任意长长为半径画弧,分别交AB,BC于点E,F;
②分别以点E,F为圆心,以大于 ![]() EF为半径画圆,两圆相交于点G,连接BG角AC于点D即可
EF为半径画圆,两圆相交于点G,连接BG角AC于点D即可
(2)解:∵在△ABC中,AB=AC,∠ABC=72°,
∴∠A=180°﹣2∠ABC=180°﹣144°=36°,
∵BD是∠ABC的平分线,
∴∠ABD= ![]() ∠ABC=
∠ABC= ![]() ×72°=36°,
×72°=36°,
∵∠BDC是△ABD的外角,
∴∠BDC=∠A+∠ABD=36°+36°=72°.
【解析】(1)根据角平分线的作法利用直尺和圆规作出∠ABC的平分线即可;(2)先根据等腰三角形的性质及三角形内角和定理求出∠A的度数,再由角平分线的定义得出∠ABD的度数,再根据三角形外角的性质得出∠BDC的度数即可.
【考点精析】通过灵活运用等腰三角形的性质,掌握等腰三角形的两个底角相等(简称:等边对等角)即可以解答此题.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:初中数学 来源: 题型:
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.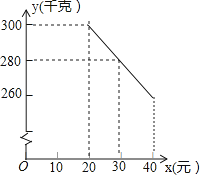
(1)求y与x的函数解析式(也称关系式)
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴相交于A,B两点,与y轴相交于点C(0,3),点B坐标是(3,0),设抛物线的顶点为点D.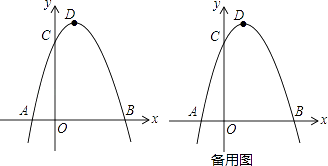
(1)求此抛物线的解析式与对称轴;
(2)作直线BC,与抛物线的对称轴交于点E,点P为直线BC上方的二次函数上一个动点(且点P与点B,C不重合),过点P作PF∥DE交直线BC于点F,设点P的横坐标为m;
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PDEF为平行四边形?
②设△PBC的面积为S,求S与m的函数关系式.S是否存在最大值?若存在,求出最大值并求出此时P点坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1). 
①以原点O为对称中心,画出△ABC关于原点O对称的△A1B1C1;
②将△ABC绕A点逆时针旋转90°得到△AB2C2 , 画出△AB2C2 , 并求出AC扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
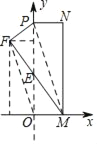
【题目】如图,在平面直角坐标系中,长方形MNPO的边OM在x轴上,边OP在y轴上,点N的坐标为(3,9),将矩形沿对角线PM翻折,N点落在F点的位置,且FM交y轴于点E,那么点F的坐标为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com