
【题目】近年来“哈罗单车”和“哈啰助力车”在街头流行.随着市民对这两种车的使用率的提升,经营“哈罗单车”和“哈啰助力车”的两家公司也有了越来越高的收人.初三某班的实践小组对两家公司近10个周的收入进行了调查,就收入(单位:千元)情况制作了如下的统计图:

根据以上信息,整理分析数据如下:
公司 | 平均周收入/千元 | 周收入中位数/千元 | 周收入众数/千元 | 方差 |
哈罗单车 | _____ | 6 | 6 | 1.2 |
哈啰助力车 | 6 | _____ | 4 | _____ |
(1)完成表格填空;
(2)“哈罗单车”和“哈啰助力车”在该地各有500辆和300辆.从收入的情况看,上个周这2家公司都达到了近10个周的最高收人.已知每骑用一次“哈罗单车”和“哈啰助力车”,公司就分别收人1元和2元,通过计算在上周每辆车的周平均骑用次数,说明哪种车比较抢手?
【答案】(1)6、4.5、7.6;(2)“哈罗助力车”比较抢手.
【解析】
(1)根据加权平均数、中位数、众数、方差的定义即可求解;
(2)计算出每辆车的周平均骑用次数进行判断即可.
解:(1) “哈罗单车”平均周收入=7×20%+8×10%+4×10%+5×20%+6×(1﹣20%﹣10%﹣10%﹣20%)=6(千克);
“哈啰助力车”周收入中位数= (4+5)÷2=4.5(千克);
“哈啰助力车” 方差=![]() ×[5×(4﹣6)2+2×(5﹣6)2+2×(9﹣6)2+(12﹣6)2]=7.6.
×[5×(4﹣6)2+2×(5﹣6)2+2×(9﹣6)2+(12﹣6)2]=7.6.
故答案为6、4.5、7.6.
(2) ∵近10个周“哈罗单车”和“哈啰助力车”的最高收入分别是8000元、12000元,
∴上周“哈罗单车”的收入是8000元、“哈啰助力车”的收入是12000元,
∴上周“哈罗单车”的平均骑用次数=8000÷500=16(次),
上周“哈啰助力车”的平均骑用次数=12000÷300÷2=20(次),
∴ “哈罗助力车”比较抢手.


科目:初中数学 来源: 题型:
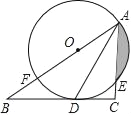
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于点D,点O在AB上,⊙O经过A、D两点,交AC于点E,交AB于点F.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径是2cm,E是弧AD的中点,求阴影部分的面积(结果保留π和根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 的图象经过点
的图象经过点![]() 、
、![]() ,顶点为
,顶点为![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
![]() 求抛物线的解析式和顶点
求抛物线的解析式和顶点![]() 的坐标;
的坐标;
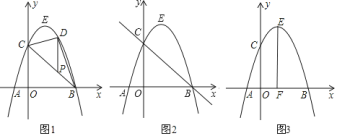
![]() 如图
如图![]() ,
,![]() 为线段
为线段![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴平行线,交抛物线于点
轴平行线,交抛物线于点![]() ,当
,当![]() 的面积最大时,求点
的面积最大时,求点![]() 的坐标;
的坐标;
![]() 如图
如图![]() ,若点
,若点![]() 是直线
是直线![]() 上的动点,点
上的动点,点![]() 、
、![]() 、
、![]() 所构成的三角形与
所构成的三角形与![]() 相似,请直接写出所有点
相似,请直接写出所有点![]() 的坐标;
的坐标;
![]() 如图
如图![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() 点,
点,![]() 是
是![]() 轴上一动点,
轴上一动点,![]() 是线段
是线段![]() 上一点,若
上一点,若![]() ,则
,则![]() 的最大值为________,最小值为________.
的最大值为________,最小值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线的表达式为![]() .
.
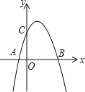
![]() 求此抛物线与
求此抛物线与![]() 轴、
轴、![]() 轴的交点坐标;
轴的交点坐标;
![]() 求抛物线与坐标轴围成的三角形的面积;
求抛物线与坐标轴围成的三角形的面积;
![]() 在上述的抛物线上是否存在这样的点
在上述的抛物线上是否存在这样的点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 点的坐标.
点的坐标.
![]() 在上述的抛物线上是否存在这样的点
在上述的抛物线上是否存在这样的点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 点的坐标.
点的坐标.
![]() 在上述的抛物线上是否存在这样的点
在上述的抛物线上是否存在这样的点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点B顺时针旋转60°得△DBE,点C的对应点E给好落在AB的延长线上,连接AD,下列结论不一定正确的是( )

A.AD∥BCB.∠DAC=∠EC.BC⊥DED.AD+BC=AE
查看答案和解析>>
科目:初中数学 来源: 题型:
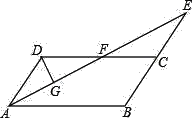
【题目】如图,在平行四边形ABCD中,∠BAD的平分线与BC的延长线交于点E,与DC交于点F.
(1)求证:CD=BE;
(2)若AB=4,点F为DC的中点,DG⊥AE,垂足为G,且DG=1,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+b的图象与直线y=x+2相交于点A(1,m)和点B(n,0).
(1)试确定二次函数的解析式;
(2)在给出的平面直角坐标系中画出这个函数图象的草图,并结合图象直接写出ax2+b>x+2时x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小红玩抛硬币游戏,连续抛两次.小明说:“如果两次都是正面,那么你赢;如果两次是一正一反,则我赢.”小红赢的概率是__________,据此判断该游戏__________(填“公平”或“不公平”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在直线l上,△ABC与△AB′C′关于直线l对称,连接BB′分别交AC,AC′于点D′,连接CC′,下列结论不一定正确的是( )
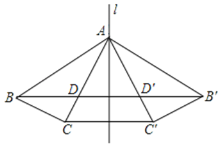
A.∠BAC=∠B′AC′B.CC′∥BB′C.BD=B′D′D.AD=DD′
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com