
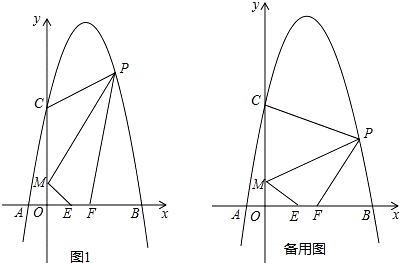
如图,对称轴为直线x=2的抛物线经过A(﹣1,0),C(0,5)两点,与x轴另一交点为B.已知M(0,1),E(a,0),F(a+1,0),点P是第 一象限内的抛物线上的动点.
一象限内的抛物线上的动点.
(1)求此抛物线的解析式;
(2)当a=1时,求四边形MEFP的面积的最大值,并求此时点P的坐标;
(3)若△PCM是以点P为顶点的等腰三角形,求a为何值时,四边形PMEF周长最小?请说明理由.
解:(1)∵对称轴为直线x=2,
∴设抛物线解析式为y=a(x﹣2)2+k.
将A(﹣1,0),C(0,5)代入得:
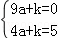 ,解得
,解得 ,
,
∴y=﹣(x﹣2)2+9=﹣x2+4x+5.
(2)当a=1时,E(1,0),F(2,0),OE=1,OF=2.
设P(x,﹣x2+4x+5),
如答图2,过点P作PN⊥y轴于点N,则PN=x,ON=﹣x2+4x+5,
∴MN=ON﹣OM=﹣x2+4x+4.
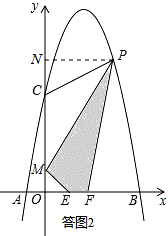
S四边形MEFP=S梯形OFPN﹣S△PMN﹣S△OME
=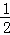 (PN+OF)•ON﹣
(PN+OF)•ON﹣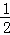 PN•MN﹣
PN•MN﹣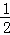 OM•OE
OM•OE
=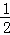 (x+2)(﹣x2+4x+5)﹣
(x+2)(﹣x2+4x+5)﹣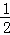 x•(﹣x2+4x+4)﹣
x•(﹣x2+4x+4)﹣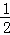 ×1×1
×1×1
=﹣x2+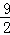 x+
x+
=﹣(x﹣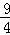 )2+
)2+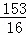
∴当x=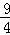 时,四边形MEFP的面积有最大值为
时,四边形MEFP的面积有最大值为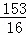 ,此时点P坐标为(
,此时点P坐标为(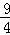 ,
,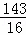 ).
).
(3)∵M(0,1),C(0,5),△PCM是以点P为顶点的等腰三角形,
∴点P的纵坐标为3.
令y=﹣x2+4x+5=3,解得x=2±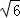 .
.
∵点P在第一象限,∴P(2+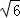 ,3).
,3).
四边形PMEF的四条边中,PM、EF长度固定,因此只要ME+PF最小,则PMEF的周长将取得最小值.
如答图3,将点M向右平移1个单位长度(EF的长度),得M1(1,1);
作点M1关于x轴的对称点M2,则M2(1,﹣1);
连接PM2,与x轴交于F点,此时ME+PF=PM2最小.

设直线PM2的解析式为y=mx+n,将P(2+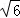 ,3),M2(1,﹣1)代入得:
,3),M2(1,﹣1)代入得:
 ,解得:m=
,解得:m=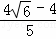 ,n=﹣
,n=﹣ ,
,
∴y= x﹣
x﹣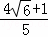 .
.
当y=0时,解得x=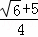 .∴F(
.∴F(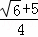 ,0).
,0).
∵a+1=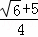 ,∴a=
,∴a= .
.
∴a= 时,四边形PMEF周长最小.
时,四边形PMEF周长最小.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
研究发现人体在注射一定剂量的某种药后的数小时内,体内血液中的药物浓度(即血药浓度)y(毫克/升)是时间t(小时)的二次函数.已知某病人的三次化验结果如下表:
| t(小时) | 0 | 1 | 2 |
| y(毫克/升) | 0 | 0.14 | 0.24 |
(1)求y与t的函数解析式;
(2)在注射后的第几个小时,该病人体内的药物浓度达到最大?最大浓度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
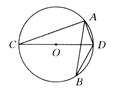
如图3-202所示,CD是⊙O的直径,A,B是⊙O上的两点.若∠ABD=20°,则∠ADC的度数为 ( )
A.40° B.50° C.60° D.70°
查看答案和解析>>
科目:初中数学 来源: 题型:
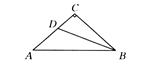
如图1—125所示,在等腰直角三角形ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=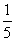 ,则AD的长为 ( )
,则AD的长为 ( )
A.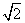 B.2 C.1 D.2
B.2 C.1 D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
为响应“节约用水”的号召,小刚随机调查了班级35名同学中5名同学家庭一年的平均用水量(单位:吨),记录如下:8,9,8,7,10,这组数据的平均数和中位数分别是( )
A.8,8 B.8.4,8 C.8.4,8.4 D.8,8.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com