

分析 (1)先用角平分线的性质定理得出DF=DE,再用HL判断出Rt△ADF≌Rt△CDE,进而得出∠DAF=∠BCD,即可得出结论;
(2)在NC上取一点H使CH=AM,借助(1)的结论判断出△ADM≌△CDH,进而判断出△MDN≌△HDN,即可得出结论;
(3)同(2)的方法的判断出△MDN≌△HDN,即可得出结论.
解答 解:(1)如图1,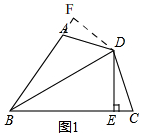
过点F作DF⊥AB,
∵BD平分∠ABC,DE⊥BC于E,
∴DF=DE,
在Rt△ADF和Rt△CDE中,$\left\{\begin{array}{l}{DF=DE}\\{AD=CD}\end{array}\right.$,
∴Rt△ADF≌Rt△CDE,
∴∠DAF=∠BCD,
∵∠BAD+∠DAF=180°,
∴∠BAD+∠BCD=180°,
(2)如图2,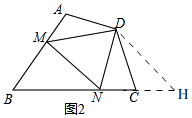
延长NC使CH=AM,连接DH,
由(1)知,∠BAD+∠BCD=180°,
∵∠BCD+∠DCM=180°,
∴∠BAD=∠HCD,
在△ADM和△CDH中,$\left\{\begin{array}{l}{AD=CD}\\{∠MAD=∠HCD}\\{AM=CH}\end{array}\right.$,
∴△ADM≌△CDH,
∴DM=DH,∠ADM=∠CDH,
∵∠BAD+∠BCD=180°,
∴∠ABC+∠ADC=180°,
∵∠ABC=50°,∠MDN=65°,
∴∠NDH=∠NDC+∠CDH=∠NDC+∠ADM=65°=∠MDN,
在△MDN和△HDN中,$\left\{\begin{array}{l}{DM=DH}\\{∠MDN=∠HDN}\\{DN=DN}\end{array}\right.$,
∴△MDN≌△HDN,
∴MN=HN=CN+CH=CN+AM;
(3)如图3,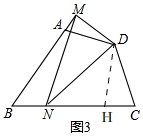
在CN上截取CH=AM,
同(2)的方法得出,△MDN≌△HDN,
∴MN=HN=CN-CH=CN-AM.
点评 此题是四边形综合题,主要考查了角平分线的性质定理,全等三角形的判定和性质,四边形的内角和,解本题的关键是得出∠MDN=∠HDN,还用到类比的思想.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,∠AOB=45°,点C在OB上,OC=8,若以点C为圆心、r为半径的圆与OA相切,则r等于( )
如图,∠AOB=45°,点C在OB上,OC=8,若以点C为圆心、r为半径的圆与OA相切,则r等于( )| A. | 4 | B. | 4$\sqrt{2}$ | C. | 4$\sqrt{3}$ | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 直线y=-x+2与X轴、y轴交于A、B两点,C在y轴的负半轴上,且OC=OB.
直线y=-x+2与X轴、y轴交于A、B两点,C在y轴的负半轴上,且OC=OB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在正方形ABCD中,点G是AD的中点,点E在AB上,满足CG⊥DE,H为CG,DE的交点,DE与对角线AC相交于点F.
在正方形ABCD中,点G是AD的中点,点E在AB上,满足CG⊥DE,H为CG,DE的交点,DE与对角线AC相交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
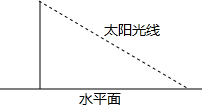 在“测量旗杆的高度”的数学课题学习中,某学习小组测得太阳光线与水平面的夹角为30°,此时旗杆在水平地面上的影子的长度为24m,则旗杆的高度约为( )
在“测量旗杆的高度”的数学课题学习中,某学习小组测得太阳光线与水平面的夹角为30°,此时旗杆在水平地面上的影子的长度为24m,则旗杆的高度约为( )| A. | 24m | B. | 20m | C. | 14m | D. | 12m |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知在Rt△ABC中,BC=6,CD是斜边AB上的中线,点G是△ABC的重心,将△ADC绕重点G旋转,得到△A1D1C1,并且C1D1∥AB,直线A1D1⊥AC,设直线A1C1、A1D1分别交AC于点E,F,那么EF的长为$\frac{5\sqrt{3}}{3}$或3$\sqrt{3}$.
已知在Rt△ABC中,BC=6,CD是斜边AB上的中线,点G是△ABC的重心,将△ADC绕重点G旋转,得到△A1D1C1,并且C1D1∥AB,直线A1D1⊥AC,设直线A1C1、A1D1分别交AC于点E,F,那么EF的长为$\frac{5\sqrt{3}}{3}$或3$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com