
����Ŀ��ijˮ�������̴������г���30Ԫÿǧ�˵ļ۸��չ���1000ǧ�˵�Ϻ���˽�г�����һ�����ڻ���ÿ��0.5Ԫÿǧ�˵ļ۸����ǣ������̴��������������������ٳ��ۣ���������һ���£�����������ڼ�Ϻ�ĸ����������ֲ��䣬��ÿ����10ǧ�˵�Ϻ��ȥ����ȥ��Ϻ���ڵ�����20Ԫÿǧ�˵ļ����۳���
��1��������10�����ۣ����Ϻ���г���Ϊÿǧ���� ��Ԫ��
��2��������x���Ϻһ�����۳�����1000ǧ�˵�Ϻ�ܹ���õ����۶�Ϊ36000Ԫ����x��ֵ��
��3���������ڼ䣬ÿ����и��������ĸ��ַ���֧��ΪaԪ���������ڷ���x���ȫ���۳�����20��x��30ʱ���������ջ��������ֵΪ1800Ԫ����a��ֵΪ�� �����ջ������������ܶ�չ��ɱ����������ã�
���𰸡���1��35Ԫ����2��x��ֵΪ20����3��a��ֵΪ210.
��������
��1��ԭ�۸������10�����ӵļ۸ɵã�
��2�����ݻ�Ϻ�����۶�+���ŵ����۶�=36000�з������ɵã�
��3���辭���������ܶ�ΪyԪ����������ó�y=��30+0.5x����1000-10x��+200x-30000-ax��20��x��30��������һ��ʽ��ó��Գ���x��![]() ���ٸ���20��x��30�����κ��������ʷ������ۼ��ɵã�
���ٸ���20��x��30�����κ��������ʷ������ۼ��ɵã�
�⣺��1��30+0.5��10��35Ԫ��
�𣺷���10�����ۣ����Ϻ���г���Ϊÿǧ��35Ԫ��
�ʴ�Ϊ��35��
��2����������30+0.5x����1000��10x��+200x��36000��
��ã�x1��20��x2��60������������ȥ����
��x��ֵΪ20��
��3���辭���������ܶ�ΪyԪ��
��������ã�y����30+0.5x����1000��10x��+200x��30000��ax����20��x��30��
������y����5x2+��400��a��x��
�Գ���x��![]()
��0��a��100ʱ����x��30ʱ��y�����ֵ��
��4500+30��400��a����1800��
���a��190����ȥ����
��a��200ʱ����x��20ʱ��y�����ֵ��
��2000+20��400��a����1800��
���a��210��
��100��a��200ʱ����x��![]() ʱ��yȡ�����ֵ��
ʱ��yȡ�����ֵ��
y���ֵ��![]() ��a2��800a+16000����
��a2��800a+16000����
�������![]() ��a2��800a+16000����1800��
��a2��800a+16000����1800��
���a��400![]() �������������⣬��ȥ����
�������������⣬��ȥ����
���ϣ�a��ֵΪ210��
�ʴ�Ϊ��210��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����AD�ǡ�O���ң���F��DA�ӳ����ϵ�һ�㣬����O��һ��C����O�����߽�DF�ڵ�E��ACƽ�֡�FAB
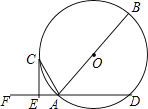
��1����֤��CE��DF����2����AE��2��CE��4�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
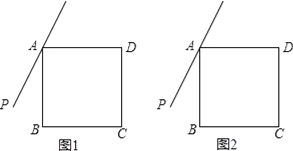
����Ŀ����������ABCD�����ֱ��AP����B����ֱ��AP�ĶԳƵ�ΪE������BE��DE������DE��ֱ��AP�ڵ�F��
��1���������ⲹȫͼ1��
������PAB=20�������ADF�Ķ�����
��2�������PAB=a����0����a��90�������ADF�Ķ�����ֱ��д�������������ú�a�Ĵ���ʽ��ʾ��
��3����ͼ2����45������PAB��90�����õ�ʽ��ʾ�߶�AB��FE��FD֮���������ϵ����֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
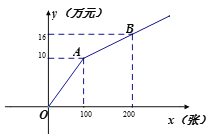
����Ŀ��ij�ݳ��Ṻ����Ʊ�ķ�ʽ������
��ʽһ:����λ��������10��Ԫ,��õ�λ������Ʊ�ļ۸�Ϊÿ��0.02��Ԫ;(ע��ʽһ���ܷ���=������+��Ʊ����)
��ʽ��:����ͼ��ʾ�Ĺ�����Ʊ��ʽ.
�蹺����Ʊx��,�ܷ���Ϊy��Ԫ.
(1)��ʽһ����ʱy��x�ĺ�����ϵʽ
(2)���ס���������λ�ֲ��÷�ʽһ����ʽ�������ݳ����Ź�400��,���ҵ�λ����100�ţ�����λ������27.2��Ԫ����ס�������λ��������Ʊ������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
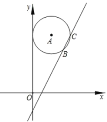
����Ŀ����ͼ����ֱ������ϵ�У���A��Բ������Ϊ��![]() ��a���뾶Ϊ
��a���뾶Ϊ![]() ������y��2x��2��ͼ��A�صõ��ҳ�Ϊ2����a��ֵΪ_____��
������y��2x��2��ͼ��A�صõ��ҳ�Ϊ2����a��ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧΪ���˽����꼶ѧ������״���������꼶ѧ���������ȡ����ѧ���������ܲ��ԣ����Խ����ΪA��B��C��D�ĸ��ȼ��������ݲ��Գɼ����������������в�������ͳ��ͼ��
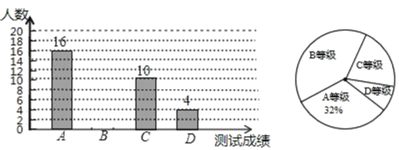
��1����γ�������������������� �����벹ȫ����ͼ��
��2��D�ȼ�ѧ������ռ�����������İٷֱ�Ϊ�� ����������ͳ��ͼ��B�ȼ�����Ӧ��Բ�Ľ�Ϊ�� ����
��3����У���꼶ѧ����1600�ˣ������������A�ȼ���ѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
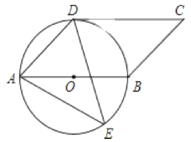
����Ŀ����ͼ����![]() �У���OΪԲ�ģ�OAΪ�뾶��Բ��BC�������B����OC�ཻ�ڵ�D��
�У���OΪԲ�ģ�OAΪ�뾶��Բ��BC�������B����OC�ཻ�ڵ�D��

��1����![]() �Ķ�����
�Ķ�����
��2����ͼ����E�ڡ�O�ϣ�����CE���O���ڵ�F����![]() ����
����![]() �Ķ�����
�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı�����ƽ���ı��Σ���ABΪֱ����![]() ������D, E��
������D, E��![]() ��һ��,��
��һ��,��![]() ��
��
(1)�ж�CD��![]() ��λ�ù�ϵ����˵������;
��λ�ù�ϵ����˵������;
(2) ��BC=2 .����Ӱ���ֵ����.(��������� ����ʽ)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2011ɽ�����ϣ�27��9�֣���ͼ������OABC�У���OΪԭ�㣬��A������Ϊ��0��8������C������Ϊ��6��0����������![]() ����A��C���㣬��AB�߽��ڵ�D��
����A��C���㣬��AB�߽��ڵ�D��
��1���������ߵĺ�������ʽ��
��2����PΪ�߶�BC��һ�����㣨�����C�غϣ�����QΪ�߶�AC��һ�����㣬AQ=CP������PQ����CP=m����CPQ�����ΪS��
����S����m�ĺ�������ʽ�������mΪ��ֵʱ��Sȡ�����ֵ��
����S���ʱ����������![]() �ĶԳ���l�������ڵ�F��ʹ��FDQΪֱ�������Σ���ֱ��д�����з���������F�����ꣻ�������ڣ���˵�����ɣ�
�ĶԳ���l�������ڵ�F��ʹ��FDQΪֱ�������Σ���ֱ��д�����з���������F�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com