
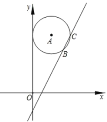
【题目】如图,在直角坐标系中,⊙A的圆心坐标为(![]() ,a)半径为
,a)半径为![]() ,函数y=2x﹣2的图象被⊙A截得的弦长为2,则a的值为_____.
,函数y=2x﹣2的图象被⊙A截得的弦长为2,则a的值为_____.
【答案】4![]() ﹣2
﹣2
【解析】
作AH⊥x轴于H,交CB于D,作AE⊥CB于E,连结AC,由题意得出![]()
![]() ,把
,把![]() 代入y=2x-2得
代入y=2x-2得![]() ,得出D点坐标为
,得出D点坐标为![]() ,得出HD=
,得出HD=![]() ,由垂径定理得出CE=BE=
,由垂径定理得出CE=BE=![]() ,由勾股定理得出
,由勾股定理得出![]() ,求出直线y=2x-2与坐标轴的交点坐标,得出OG=2,OF=1,由平行线的性质得出∠ADE=∠HDF=∠OGF,求出DE=2AE=4,由勾股定理得出
,求出直线y=2x-2与坐标轴的交点坐标,得出OG=2,OF=1,由平行线的性质得出∠ADE=∠HDF=∠OGF,求出DE=2AE=4,由勾股定理得出![]() ,即可得出结果.
,即可得出结果.
解:作AH⊥x轴于H,交CB于D,作AE⊥CB于E,连结AC,如图,

∵⊙A的圆心坐标为(![]() ,a),
,a),
∴OH=![]() ,AH=a,
,AH=a,
把x=![]() 代入y=2x﹣2得y=2
代入y=2x﹣2得y=2![]() ﹣2,
﹣2,
∴D点坐标为(![]() ,2
,2![]() ﹣2),
﹣2),
∴HD=2![]() ﹣2,
﹣2,
∵AE⊥CB,
∴CE=BE=![]() ,
,
在Rt△ACE中,AC=![]() ,
,
∴![]() ,
,
∵span>y=2x﹣2,
当x=0时,y=﹣2;当y=0时,x=1,
∴G(0,﹣2),F(1,0),
∴OG=2,OF=1,
∵AH∥y轴,
∴∠ADE=∠CDF=∠OGF,
∴tan∠ADE=![]() =tan∠OGF=
=tan∠OGF=![]() =
=![]() ,
,
∴DE=2AE=4,
∴AD=![]() =
=![]() =2
=2![]() ,
,
∴a=AH=AD+HD=2![]() +2
+2![]() ﹣2=4
﹣2=4![]() ﹣2,
﹣2,
故答案为:4![]() ﹣2.
﹣2.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:
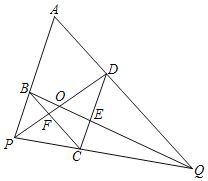
【题目】如图, 已知菱形![]() ,
,![]() ,点
,点![]() 是边
是边![]() 延长线上一点, 连接
延长线上一点, 连接![]() 交
交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 、
、![]() 于点
于点![]() 、
、![]() ,设
,设![]() ,
,![]() .
.
(1)用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)求![]() 关于
关于![]() 的函数解析式, 并写出它的定义域;
的函数解析式, 并写出它的定义域;
(3)当![]() 与
与![]() 相似时, 求
相似时, 求![]() 的值 .
的值 .
查看答案和解析>>
科目:初中数学 来源: 题型:
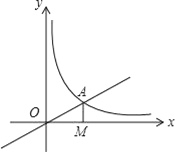
【题目】如图,直线OA:y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() (k≠0)在第一象限的图象交于A点,过A点作轴的垂线,垂足为M,已知△OAM的面积为1.
(k≠0)在第一象限的图象交于A点,过A点作轴的垂线,垂足为M,已知△OAM的面积为1.
(1)求反比例函数的解析式;
(2)如果B为反比例函数在第一象限图象上的点(点B与点A不重合),且B点的横坐标为1,在x轴上求一点P,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
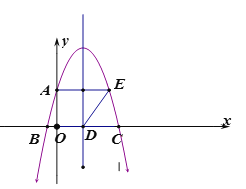
【题目】已知:如图抛物线y=ax2+bx+![]() 与y轴交于点A,与x轴交于点B、点C.连接AB,以AB为边向右作平行四边形ABDE,点E落在抛物线上,点D落在x轴上,若抛物线的对称轴恰好经过点D,且∠ABD=60°,则这条抛物线的解析式为( )
与y轴交于点A,与x轴交于点B、点C.连接AB,以AB为边向右作平行四边形ABDE,点E落在抛物线上,点D落在x轴上,若抛物线的对称轴恰好经过点D,且∠ABD=60°,则这条抛物线的解析式为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点A为⊙0外一点,过A作⊙O的切线与⊙O相切于点P,连接PO并延长至圆上一点B连接AB交⊙O于点C,连接OA交⊙O于点D连接DP且∠OAP=∠DPA。
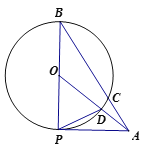
(1)求证:PO=PD
(2)若AC=![]() ,求⊙O的半径。
,求⊙O的半径。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水产经销商从批发市场以30元每千克的价格收购了1000千克的虾,了解到市场价在一个月内会以每天0.5元每千克的价格上涨,经销商打算先在塘里放养几天后再出售(但不超过一个月).假设放养期间虾的个体质量保持不变,但每天有10千克的虾死去.死去的虾会在当天以20元每千克的价格售出.
(1)若放养10天后出售,则活虾的市场价为每千克 元.
(2)若放养x天后将活虾一次性售出,这1000千克的虾总共获得的销售额为36000元,求x的值.
(3)若放养期间,每天会有各种其他的各种费用支出为a元,经销商在放养x天后全部售出,当20≤x≤30时,经销商日获利的最大值为1800元,则a的值为 (日获利=日销售总额﹣收购成本﹣其他费用)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现如今,“垃圾分类”意识已深入人心,垃圾一般可分为:可回收物、厨余垃圾、有害垃圾、其它垃圾.其中甲拿了一袋垃圾,乙拿了两袋垃圾.
(1)直接写出甲所拿的垃圾恰好是“厨余垃圾”的概率;
(2)求乙所拿的两袋垃圾不同类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
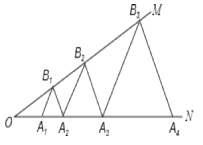
【题目】如图,已知:∠MON=30°,点A![]() 、A
、A![]() 、A
、A![]() …在射线ON上,点B
…在射线ON上,点B![]() 、B
、B![]() 、B
、B![]() …在射线OM上,△A
…在射线OM上,△A![]() B
B![]() A
A![]() 、△A
、△A![]() B
B![]() A
A![]() 、△A
、△A![]() B
B![]() A
A![]() …均为等边三角形,若OA
…均为等边三角形,若OA![]() =1,则△A
=1,则△A![]() B
B![]() A
A![]() 的边长为____
的边长为____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列图形:

它们是按一定规律排列的,依照此规律,第5个图形中的五角星的个数为___,第n个图形中的五角星(n为正整数)个数为____(用含n的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com