
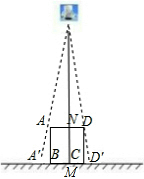
 如图,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的部分影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为180cm.
如图,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的部分影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为180cm. 分析 先证明△A′AB∽△A′OM得到$\frac{A′B}{A′B+BM}$=$\frac{30}{OM}$①,再证明△D′DC∽△D′OM得到$\frac{D′C}{D′C+CM}$=$\frac{30}{OM}$②,则利用等量代换和比例性质得$\frac{A′B}{A′B+BM}$=$\frac{D′C}{D′C+CM}$$\frac{A′B+D′C}{A′B+BM+CM+D′C}$=$\frac{1}{6}$,所以$\frac{30}{OM}$=$\frac{1}{6}$,于是易得OM=180.
解答 解: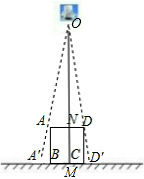 如图,
如图,
∵AB∥OM,
∴△A′AB∽△A′OM,
∴$\frac{A′B}{A′M}$=$\frac{AB}{OM}$,即$\frac{A′B}{A′B+BM}$=$\frac{30}{OM}$①,
∵DC∥OM,
∴△D′DC∽△D′OM,
∴$\frac{D′C}{D′M}$=$\frac{CD}{OM}$,即$\frac{D′C}{D′C+CM}$=$\frac{30}{OM}$②,
由①②得$\frac{A′B}{A′B+BM}$=$\frac{D′C}{D′C+CM}$,
∴$\frac{A′B}{A′B+BM}$=$\frac{D′C}{D′C+CM}$=$\frac{A′B+D′C}{A′B+BM+CM+D′C}$=$\frac{6}{30+6}$=$\frac{1}{6}$,
∴$\frac{30}{OM}$=$\frac{1}{6}$,
∴OM=180(cm).
故答案为180.
点评 本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度(测量距离);借助标杆或直尺测量物体的高度.也考查了比例性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:选择题
 如图,△ABC中,点D,E,F分别在三边上,DE∥CA,DF∥BA.下列四个判断不正确的是( )
如图,△ABC中,点D,E,F分别在三边上,DE∥CA,DF∥BA.下列四个判断不正确的是( )| A. | 四边形AEDF是平行四边形 | |
| B. | 如果∠BAC=90°,那么四边形AEDF是矩形 | |
| C. | 如果AD平分∠BAC,那么四边形AEDF是矩形 | |
| D. | 如果AD⊥BC,且AB=AC,那么四边形AEDF是菱形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
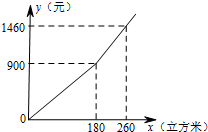 为增强居民的节水意识,某市自2014年实施“阶梯水价”.按照“阶梯水价”的收费标准,居民家庭每年应缴水费y(元)与用水量x(立方米)的函数关系的图象如图所示.如果某个家庭2014年全年上缴水费1180元,那么该家庭2014年用水的总量是( )
为增强居民的节水意识,某市自2014年实施“阶梯水价”.按照“阶梯水价”的收费标准,居民家庭每年应缴水费y(元)与用水量x(立方米)的函数关系的图象如图所示.如果某个家庭2014年全年上缴水费1180元,那么该家庭2014年用水的总量是( )| A. | 240立方米 | B. | 236立方米 | C. | 220立方米 | D. | 200立方米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
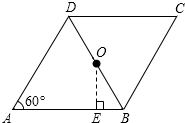 如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.则线段BE的长是( )
如图,在菱形ABCD中,∠A=60°,AB=4,O为对角线BD的中点,过O点作OE⊥AB,垂足为E.则线段BE的长是( )| A. | 1 | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
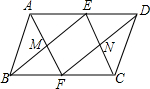 已知:如图,在?ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N,AF,BE分别平分∠BAD,∠ABC;CE,DF分别平分∠BCD,∠ADC,则四边形MFNE是( )
已知:如图,在?ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N,AF,BE分别平分∠BAD,∠ABC;CE,DF分别平分∠BCD,∠ADC,则四边形MFNE是( )| A. | 菱形 | B. | 矩形 | C. | 平行四边形 | D. | 正方形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com