
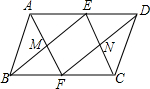
 已知:如图,在?ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N,AF,BE分别平分∠BAD,∠ABC;CE,DF分别平分∠BCD,∠ADC,则四边形MFNE是( )
已知:如图,在?ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N,AF,BE分别平分∠BAD,∠ABC;CE,DF分别平分∠BCD,∠ADC,则四边形MFNE是( )| A. | 菱形 | B. | 矩形 | C. | 平行四边形 | D. | 正方形 |
科目:初中数学 来源: 题型:填空题
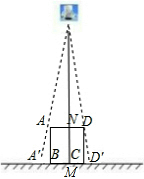 如图,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的部分影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为180cm.
如图,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的部分影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为180cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
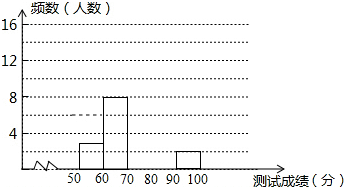 为了增强学生环保意识,我区举办了首届“环保知识大赛”,经选拔后有30名学生参加决赛,这30,名学生同事解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了增强学生环保意识,我区举办了首届“环保知识大赛”,经选拔后有30名学生参加决赛,这30,名学生同事解答50个选择题,若每正确一个选择题得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 50≤x<60 | 3 |
| 第2组 | 60≤x<70 | 8 |
| 第3组 | 70≤x<80 | 13 |
| 第4组 | 80≤x<90 | a |
| 第5组 | 90≤x<100 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
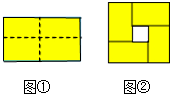 图①是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图②那样拼成一个正方形,则中间空的部分的面积是( )
图①是一个长为2m,宽为2n(m>n)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图②那样拼成一个正方形,则中间空的部分的面积是( )| A. | (m-n)2 | B. | (m+n)2 | C. | 2mn | D. | m2-n2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
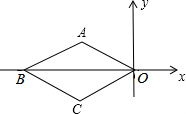 如图,菱形ABCO中AO=$\sqrt{3}$,∠AOC=60°,点M第一次从点O移动到点A,第二次从点A移动到点B,第三次从点B移动到点C,第四次从点C移动到点O…照此移动规律,点M第39次移动到的点的坐标是(-$\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$).
如图,菱形ABCO中AO=$\sqrt{3}$,∠AOC=60°,点M第一次从点O移动到点A,第二次从点A移动到点B,第三次从点B移动到点C,第四次从点C移动到点O…照此移动规律,点M第39次移动到的点的坐标是(-$\frac{3}{2}$,-$\frac{\sqrt{3}}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 每天使用零花钱(单位:元) | 1 | 2 | 3 | 4 | 5 |
| 人数 | 1 | 3 | 6 | 5 | 5 |
| A. | 3,3 | B. | 3,3.5 | C. | 3.5,3.5 | D. | 3.5,3 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{5}{3}$ | B. | $\frac{5}{3}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com