

���� ��1����ʾ���ĸ��ڽǼ��ĸ���ǣ��̶��������жϣ�
��2���ֱ��ʾ����1����2����3����4����5�������ڽ��С�1��С������С�8����жϡ�8�Ǻ͡�1���ڵ���ǣ��̶��ɵó����ۣ�
��3������ȱ�������ABC���ڽǼ���ǣ�ͬ��2����ʾ�����ǣ�Ѱ�ҹ�ϵ������ȷ�����ۣ�
��� �⣺��1�������⣮
��ƽ���ı���ABCD���ĸ��ڽǷֱ��ǡ�A=x����B=180-x����C=x����D=180-x��
���Ӧ���ĸ���Ƕ����ֱ�Ϊ180-x��x��180-x��x��
�ĸ��ڽǺ��ĸ���ǰ���С����������ȫ��ȣ��������ǵı���ȣ�
����ƽ���ı���һ��������ȱ��ı����������⣮
��2��a+d=b+c��
������ȱ��ı��ε��ĸ���Ƿֱ�Ϊ��5����6����7����8��
�ߡ�1����2����3����4=��5����6����7����8=a��b��c��d��
�ߡ�1+��2+��3+��4=��5+��6+��7+��8=360�㣬
���1=$\frac{a}{a+b+c+d}$��360��=��5��ͬ����2=��6����3=��7����4=��8��
���ڽ��С�1��С������С�8���
���8�Ǻ͡�1���ڵ���ǣ�
���1+��8=180�㣮
����1+��4=180�㣬
���2+��3=180�㣬�Ӷ���1+��4=��2+��3��
Ҳ��$\frac{a}{a+b+c+d}$��360+$\frac{d}{a+b+c+d}$��360=$\frac{b}{a+b+c+d}$��360+$\frac{c}{a+b+c+d}$��
����a+d=b+c��
��3��������ȱ�������ABC�������ڽǷֱ��ǡ�1����2����3����1����2����3=a��b��c��a��b��c��������������Ƿֱ��ǡ�4����5����6
�ߡ�1����2����3=��4����5����6=a��b��c����1+��2+��3=180�㣬��4+��5+��6=360��
���1=$\frac{a}{a+b+c}$��180����2=$\frac{b}{a+b+c}$��180����3=$\frac{c}{a+b+c}$��180��
��4=$\frac{a}{a+b+c}$��360����5=$\frac{b}{a+b+c}$��360����6=$\frac{c}{a+b+c}$��360��
���4=2��1����5=2��2����6=2��3��
���ڽ��С�1��С������С�6���
���1+��6=180
�ڽ��С�3�������С�4��С��
���3+��4=180��
���1+2��3=180 ��
��3+2��1=180 ��
��-�ڵá�3-��1=0������3=��1����a=c��
��a��b��c
��a=b=c
��������ȱ�������ֻ���ǵȱ������Σ�
������������ֻ�еȱ�������������ȱ������Σ�
���� ���⿼�����ı��ε��ۺϣ��ѶȽϴ���Ҫһ���������������������Ҫ��ѧ���������ն��������ǵ����ʣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{3}$ | B�� | $\sqrt{2}$ | C�� | 2 | D�� | 2$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
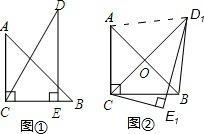 ������б�߳���ȵ�ֱ��������ֽƬ��ͼ�ٷ��ã����С�ACB=��CED=90�㣮��A=45�㣬��D=30�㣮
������б�߳���ȵ�ֱ��������ֽƬ��ͼ�ٷ��ã����С�ACB=��CED=90�㣮��A=45�㣬��D=30�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
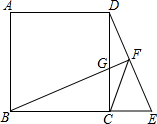 ��ͼ����EΪ������ABCD�ı�BC�ӳ�����һ�㣬BF��DE�ڵ�F����CD���ڵ�G��
��ͼ����EΪ������ABCD�ı�BC�ӳ�����һ�㣬BF��DE�ڵ�F����CD���ڵ�G���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{2015}$ | B�� | $\frac{1}{2015}$ | C�� | 5102 | D�� | 2015 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com