
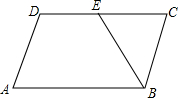
 如图,在平行四边形ABCD中,AB=8,AD=5,sinA=$\frac{4}{5}$,E是DC上的一点,且BE=BC,则DE的长为2.
如图,在平行四边形ABCD中,AB=8,AD=5,sinA=$\frac{4}{5}$,E是DC上的一点,且BE=BC,则DE的长为2. 分析 作BF⊥CD于F.先由平行四边形的性质得出CD=AB=8,BC=AD=5,sinC=sinA=$\frac{4}{5}$,再解直角△BCF,由sinC=$\frac{BF}{BC}$=$\frac{4}{5}$,求出BF=$\frac{4}{5}$BC=4,利用勾股定理得到CF=$\sqrt{B{C}^{2}-B{F}^{2}}$=3,然后根据等腰三角形三线合一的性质得出CE=2CF=6,那么DE=CD-CE=2.
解答 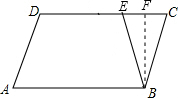 解:如图,作BF⊥CD于F.
解:如图,作BF⊥CD于F.
∵在平行四边形ABCD中,AB=8,AD=5,sinA=$\frac{4}{5}$,
∴CD=AB=8,BC=AD=5,sinC=sinA=$\frac{4}{5}$,
在直角△BCF中,∵∠BFC=90°,
∴sinC=$\frac{BF}{BC}$=$\frac{4}{5}$,
∴BF=$\frac{4}{5}$BC=4,
∴CF=$\sqrt{B{C}^{2}-B{F}^{2}}$=3.
∵BE=BC,BF⊥CD于F,
∴CE=2CF=6,
∴DE=CD-CE=8-6=2.
故答案为2.
点评 本题考查了平行四边形的性质,解直角三角形,等腰三角形的性质,准确作出辅助线求出CF的长是解题的关键.


科目:初中数学 来源: 题型:解答题
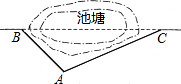 市政府为了改善城市交通环境,在如图所示的池塘B、C两点之间修建起一条公路桥(如图),经测量原路中的AB=6km,∠ABC=45°,∠ACB=30°,若一辆汽车的耗油量为0.2升/km,那么现在一辆汽车每通过一次新桥(BC)可以比走原路(BAC)节省多少升油?(结果保留根号)
市政府为了改善城市交通环境,在如图所示的池塘B、C两点之间修建起一条公路桥(如图),经测量原路中的AB=6km,∠ABC=45°,∠ACB=30°,若一辆汽车的耗油量为0.2升/km,那么现在一辆汽车每通过一次新桥(BC)可以比走原路(BAC)节省多少升油?(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
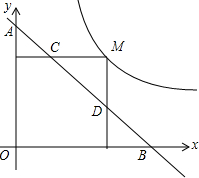 如图,反比例函数$y=\frac{k}{x}$经过点(1,$\sqrt{3}$),则k=$\sqrt{3}$;若点M为该曲线上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为2$\sqrt{3}$.
如图,反比例函数$y=\frac{k}{x}$经过点(1,$\sqrt{3}$),则k=$\sqrt{3}$;若点M为该曲线上的一点,过点M作x轴、y轴的垂线,分别交直线y=-x+m于点D、C两点,若直线y=-x+m与y轴交于点A,与x轴相交于点B,则AD•BC的值为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com