
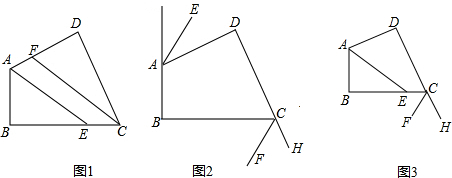
���� ��1�����ͼ����ͼ1��AE��CF��λ�ù�ϵ��
��2�����ͼ����ͼ2��AE��CF��λ�ù�ϵ��
��3�����ͼ����ͼ3��AE��CF��λ�ù�ϵ��
��4��ͼ1�У������ı��ε��ڽǺ���360�㣬�ɵá�1+��2+��3+��4�Ķ��������ݽ�ƽ���ߵĶ��壬�ɵá�1���3���࣬���������ε��ڽǺͶ����á�1���5Ҳ���࣬ͬ�ǵ������ȣ��ó���3=��5������ͬλ�������ֱ��ƽ�У���֤AE��FC��
��� �⣺��1��ͼ1��AE��FC��
��2��ͼ2��AE��FC��
��3��ͼ3��AE��FC��
��4��ѡ��ͼ1֤������ͼ1��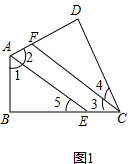
�ߡ�BAD+��BCD=��1+��2+��3+��4=360��-����B+��D��=360��-180��=180�㣬
�֡�AE��CF�ֱ��ǡ�BAD�͡�DCB���ڽ�ƽ���ߣ�
���1+��3=$\frac{1}{2}$��BAD+$\frac{1}{2}$��BCD=$\frac{1}{2}$����BAD+��BCD��=$\frac{1}{2}$��180��=90�㣮
�֡ߡ�B=90�㣬
���1+��5=90�㣬
���3=��5��
��AE��FC��
ѡ��ͼ2֤������ͼ2��
�ߡ�B=��D=90�㣬
���BAD+��BCD=360��-2��90��=180�㣬
��$\frac{1}{2}$��BAD+$\frac{1}{2}$��BCD=90�㣬
���GAD=��BCD��
��AE�ǡ�GAD�Ľ�ƽ���ߣ�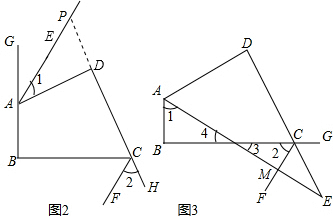
���1=$\frac{1}{2}$��GAD=$\frac{1}{2}$��BCD��
ͬ���ɵã���2=$\frac{1}{2}$��BAD��
���1+$\frac{1}{2}$��BAD=90�㣬
�ӳ�CD��AE�ڵ�P����ADC=90�㣬
���1+��P=90�㣬
���P=$\frac{1}{2}$��BAD��
����P=��2��
��AE��FC��ͬλ����ȣ���ֱ��ƽ�У���
ѡ��ͼ3֤������ͼ3��
�ߡ�B+��BAD+��D+��DCB=360�㣬
�֡ߡ�B=��D=90�㣬
���BAD+��DCB=180�㣬
�ߡ�DCB+��BCE=180�㣬
���BAD=��BCE��
��AE��AF�ֱ��ǡ�BAD�͡�DCB���ڽ�ƽ���ߺ����ƽ���ߣ�
���1=$\frac{1}{2}$��BAD����2=$\frac{1}{2}$��BCE��
���1=��2��
�ߡ�3=��4����1+��B+��4=180�㣬��2+��CMA+��3=180�㣬
�ߡ�B=90���1+��4=��2+��3��
���CMA=��B=90��
�ʴ�Ϊ��AE��FC��AE��FC��AE��FC��
���� �����˶�����ڽ�����ǣ�ƽ���ߵ����ʣ��������ڽǺͶ�����������Ҫ�ж���ֱ��ƽ�е��⣬��Χ�ƽ�����ͬλ�ǡ��ڴ��Ǻ�ͬ���ڽǣ�������һ��̽����������������Ŀ������Ч������ѧ����ִ������˼ά��ʽ��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{5}{3}$ | B�� | -4 | C�� | $\frac{7}{3}$ | D�� | $\frac{1}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
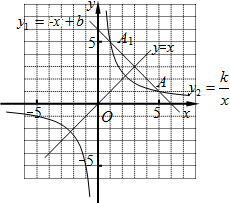 ��ͼ���ڷ���ֽ�н���ֱ������ϵ����֪һ�κ���y1=-x+b��ͼ���뷴��������y2=$\frac{k}{x}$��ͼ���ཻ�ڵ�A��5��1����A1������A��A1����ֱ��y=x�Գƣ���ͼ��ɵò���ʽ$\frac{k}{x}$+x-b��0�Ľ��ǣ�������
��ͼ���ڷ���ֽ�н���ֱ������ϵ����֪һ�κ���y1=-x+b��ͼ���뷴��������y2=$\frac{k}{x}$��ͼ���ཻ�ڵ�A��5��1����A1������A��A1����ֱ��y=x�Գƣ���ͼ��ɵò���ʽ$\frac{k}{x}$+x-b��0�Ľ��ǣ�������| A�� | x��5 | B�� | 0��x��-1 | C�� | 1��x��5 | D�� | x��5�� 0��x��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
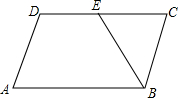 ��ͼ����ƽ���ı���ABCD�У�AB=8��AD=5��sinA=$\frac{4}{5}$��E��DC�ϵ�һ�㣬��BE=BC����DE�ij�Ϊ2��
��ͼ����ƽ���ı���ABCD�У�AB=8��AD=5��sinA=$\frac{4}{5}$��E��DC�ϵ�һ�㣬��BE=BC����DE�ij�Ϊ2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
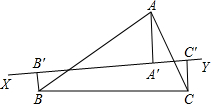 ��ͼ������ABC������G��ֱ��XY��ʹA��B��C��XY����࣬�Ӷ���A��B��C������ֱ�������ߣ��费��ֱ�Ϊ��A�䣬B�䣬C�䣬��֤��AA��=BB��+CC�䣮
��ͼ������ABC������G��ֱ��XY��ʹA��B��C��XY����࣬�Ӷ���A��B��C������ֱ�������ߣ��费��ֱ�Ϊ��A�䣬B�䣬C�䣬��֤��AA��=BB��+CC�䣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2011 | B�� | 2012 | C�� | 2013 | D�� | 2014 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com