
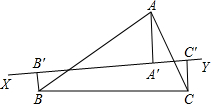
 如图,过△ABC的重心G引直线XY,使A与B,C在XY的异侧,从顶点A,B,C向这条直线作垂线,设垂足分别为如A′,B′,C′,求证:AA′=BB′+CC′.
如图,过△ABC的重心G引直线XY,使A与B,C在XY的异侧,从顶点A,B,C向这条直线作垂线,设垂足分别为如A′,B′,C′,求证:AA′=BB′+CC′. 分析 连接AG并延长交BC于D,过D作DE⊥XY于E,通过△AA′G∽△DEG,得到$\frac{AA′}{DE}=\frac{AG}{DG}$,由于点G是△ABC的重心,于是得到$\frac{AG}{DG}=2$,BD=CD,然后根据梯形的中位线定理得到结论.
解答 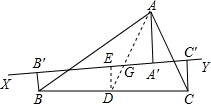 解:连接AG并延长交BC于D,过D作DE⊥XY于E,
解:连接AG并延长交BC于D,过D作DE⊥XY于E,
∵AA′⊥XY,
∴∠AA′G=∠DEG=90°,∠AGA′=∠DGE,
∴△AA′G∽△DEG,
∴$\frac{AA′}{DE}=\frac{AG}{DG}$,
∵点G是△ABC的重心,
∴$\frac{AG}{DG}=2$,BD=CD,
∴AA′=2DE,
∵BB′⊥XY,CC′⊥XY,
∴BB′∥DE∥CC′,
∴BB′+CC′=2DE,
∴AA′=BB′+CC′.
点评 本题考查了梯形中位线定理,三角形的重心,作辅助线构成梯形中位线是解题的关键.


科目:初中数学 来源: 题型:填空题
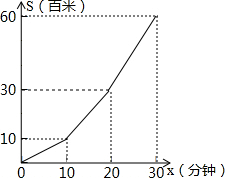 小明利用星期六、日双休骑自行车到城外小姨家去玩.星期六从家中出发,先上坡,后走平路,再走下坡路到小姨家.行程情况如图所示.星期日小明又沿原路返回自己家.若两天中,小明上坡、平路、下坡行驶的速度相对不变,则星期日,小明返回家的时间是43$\frac{1}{3}$分钟.
小明利用星期六、日双休骑自行车到城外小姨家去玩.星期六从家中出发,先上坡,后走平路,再走下坡路到小姨家.行程情况如图所示.星期日小明又沿原路返回自己家.若两天中,小明上坡、平路、下坡行驶的速度相对不变,则星期日,小明返回家的时间是43$\frac{1}{3}$分钟.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
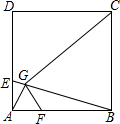 如图,在正方形ABCD中,点E、F分别在边AD、AB上,且AE=AF,AG⊥BE于点G.求证:
如图,在正方形ABCD中,点E、F分别在边AD、AB上,且AE=AF,AG⊥BE于点G.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 补贴数额(元) | 10 | 20 | … |
| 种植亩数(亩) | 160 | 240 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com