
| 补贴数额(元) | 10 | 20 | … |
| 种植亩数(亩) | 160 | 240 | … |
分析 (1)首先根据已知条件和表格数据利用待定系数法可以求出y与x之间的函数关系式,又随着补贴数额x的不断增大,种植规模也不断增加,但每亩牡丹的收益z(元)会相应降低,且该县补贴政策实施前每亩牡丹的收益为3000元,而每补贴10元(补贴数为10元的整数倍),每亩牡丹的收益会相应减少30元,由此可以得到z=3000-$\frac{x}{10}$×30,化简即可得到函数关系式;
(2)根据题目条件知道W=y•z,然后分别把(1)中的函数关系式代入其中即可得到W关于x的二次函数,然后利用二次函数的性质即可解决问题;
(3)此时平均每亩收益$\frac{6120000}{4000}$(元),设混种牡丹的土地m亩,则根据题意可以列出方程(1530+2000)•m-530m-25m2=80000,解方程即可求出m,也就求出了混种牡丹的土地有多少亩.
解答 解:(1)y=kx+b过(10,160)(20,240)
∴$\left\{\begin{array}{l}{160=10k+b}\\{240=20k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=8}\\{b=80}\end{array}\right.$,
∴y=8x+80,
z=3000-$\frac{x}{10}$•30=-3x+3000;
(2)W=y•z=(8x+80)(-3x+3000)=-24x2+23760x+240000,
当x=495时,W最大,
∵x为10的整数倍,
∴当x=490或x=500时,W最大=6120000,
∵从政府角度出发,
∴当x=490时,W最大=6120000,
此时种植y=8×490+80=4000亩;
(3)此时平均每亩收益$\frac{6120000}{4000}$=1530(元),
设混种花木的土地m亩,则
(1530+2000)•m-530m-25m2=80000,
m2-120m+3200=0,
解得:m=60±20,
∴m1=60+20=80>50,
m2=60-20=40,
∴混种花木的土地有40亩.
点评 本题分别考查了二次函数在实际生活中的应用、一元二次方程在实际中的应用、待定系数法确定一次函数的解析式等知识,综合性比较强,解题时首先要正确理解题意,准确把握题目中的数量关系,利用这些数量关系分别确定函数关系式和列出方程解决问题.


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
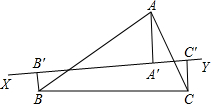 如图,过△ABC的重心G引直线XY,使A与B,C在XY的异侧,从顶点A,B,C向这条直线作垂线,设垂足分别为如A′,B′,C′,求证:AA′=BB′+CC′.
如图,过△ABC的重心G引直线XY,使A与B,C在XY的异侧,从顶点A,B,C向这条直线作垂线,设垂足分别为如A′,B′,C′,求证:AA′=BB′+CC′.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
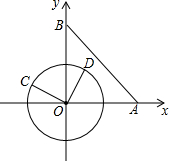 在平面直角坐标系xOy中,已知点A(6,0)、点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列)连接AB
在平面直角坐标系xOy中,已知点A(6,0)、点B(0,6),动点C在以半径为3的⊙O上,连接OC,过O点作OD⊥OC,OD与⊙O相交于点D(其中点C、O、D按逆时针方向排列)连接AB查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1次 | B. | 50次 | C. | 100次 | D. | 200次 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠B=30° | B. | 斜边上的中线长为1 | ||
| C. | 该三角形外接圆的半径为1 | D. | 斜边上高线长为$\frac{2}{5}\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
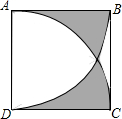 如图,正方形ABCD的边长为1,分别以A、D为圆心,1为半径画弧BD、AC,则图中阴影部分的面积$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.
如图,正方形ABCD的边长为1,分别以A、D为圆心,1为半径画弧BD、AC,则图中阴影部分的面积$\frac{\sqrt{3}}{2}$-$\frac{π}{6}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com