
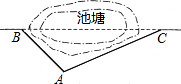
 市政府为了改善城市交通环境,在如图所示的池塘B、C两点之间修建起一条公路桥(如图),经测量原路中的AB=6km,∠ABC=45°,∠ACB=30°,若一辆汽车的耗油量为0.2升/km,那么现在一辆汽车每通过一次新桥(BC)可以比走原路(BAC)节省多少升油?(结果保留根号)
市政府为了改善城市交通环境,在如图所示的池塘B、C两点之间修建起一条公路桥(如图),经测量原路中的AB=6km,∠ABC=45°,∠ACB=30°,若一辆汽车的耗油量为0.2升/km,那么现在一辆汽车每通过一次新桥(BC)可以比走原路(BAC)节省多少升油?(结果保留根号) 分析 首先过点A作AD⊥BC于D,进而得出AB的长,进而得出BD、AC、CD的长即可得出答案.
解答 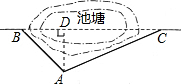 解:过点A作AD⊥BC于D
解:过点A作AD⊥BC于D
在直角三角形ADB中,$sin45°=\frac{AD}{AB}$,
∴AB=$6×\frac{{\sqrt{2}}}{2}=3\sqrt{2}$(km),
∴BD=AB=$3\sqrt{2}$(km),
在直角三角形ADC中,
AC=$6\sqrt{2}$$cos30°=\frac{CD}{AC}$,
∴CD=$6\sqrt{2}×\frac{{\sqrt{3}}}{2}=3\sqrt{6}$(km
现在一辆汽车每通过一次新桥(BC)可以比走原路(BAC)节省油的升数为:$({6+6\sqrt{2}-3\sqrt{2}-3\sqrt{6}})×\frac{1}{5}=\frac{6}{5}+\frac{{3\sqrt{2}}}{5}-\frac{{3\sqrt{6}}}{5}$,
答:现在一辆汽车每通过一次新桥(BC)可以比走原路(BAC)节省油($\frac{6}{5}+\frac{{3\sqrt{2}}}{5}-\frac{{3\sqrt{6}}}{5}$)升.
点评 此题主要考查了解直角三角形的应用,根据题意正确构造直角三角形是解题关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
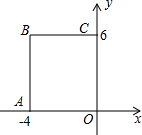 如图,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,A(-4,0),C(0,6),如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{4}$,那么点B的对应点B′的坐标是(-2,3)或(2,-3).
如图,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,A(-4,0),C(0,6),如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{4}$,那么点B的对应点B′的坐标是(-2,3)或(2,-3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 年级 | 七年级 | 八年级 | 九年级 |
| 捐款(元) | 7680 | 7700 | 7590 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | AB=DE,∠A=∠D,BC=EF | B. | AB=EF,∠A=∠D,AC=DF | ||
| C. | AB=BC,∠B=∠E,DE=EF | D. | BC=EF,∠C=∠F,AC=DF |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{5}{3}$ | B. | -4 | C. | $\frac{7}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com