
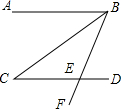
 如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠CEF的度数是70°.
如图,已知AB∥CD,BC平分∠ABE,∠C=35°,则∠CEF的度数是70°.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
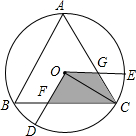 如图,△ABC是⊙O的内接等边三角形,⊙O的半径0D、OE分别交BC、CA于点F、G,∠DOE=120°.探索四边形0FCG的面积(图中阴影部分)与△ABC面积之间的数量关系,并说明理由(提示:连接0B、OC)
如图,△ABC是⊙O的内接等边三角形,⊙O的半径0D、OE分别交BC、CA于点F、G,∠DOE=120°.探索四边形0FCG的面积(图中阴影部分)与△ABC面积之间的数量关系,并说明理由(提示:连接0B、OC)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
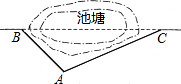 市政府为了改善城市交通环境,在如图所示的池塘B、C两点之间修建起一条公路桥(如图),经测量原路中的AB=6km,∠ABC=45°,∠ACB=30°,若一辆汽车的耗油量为0.2升/km,那么现在一辆汽车每通过一次新桥(BC)可以比走原路(BAC)节省多少升油?(结果保留根号)
市政府为了改善城市交通环境,在如图所示的池塘B、C两点之间修建起一条公路桥(如图),经测量原路中的AB=6km,∠ABC=45°,∠ACB=30°,若一辆汽车的耗油量为0.2升/km,那么现在一辆汽车每通过一次新桥(BC)可以比走原路(BAC)节省多少升油?(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 对旅客上飞机前的安检 | B. | 了解全班同学每周体育锻炼的时间 | ||
| C. | 企业招聘,对应聘人员的面试 | D. | 了解某批次灯泡的使用寿命情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
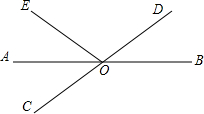 补全解答过程:
补全解答过程:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com