
分析 (1)(2)先化简再相加即可求解;
(3)(4)(5)(6)先根据加法交换律把同分母分数交换,再根据加法结合律进行计算.
解答 解:(1)3+(-1)+(-3)+1+(-4)
=3-1-3+1-4
=(3-3)+(-1+1)-4
=0+0-4
=-4;
(2)(-9)+4+(-5)+8
=-9+4-5+8
=(-9-5)+(4+8)
=-14+12
=-2;
(3)(-36.35)+(-7.25)+26.35+(+7$\frac{1}{4}$)
=(-36.35+26.35)+(-7.25+7$\frac{1}{4}$)
=-10+0
=-10;
(4)$\frac{5}{9}$+1$\frac{5}{6}$+$\frac{4}{9}$+(-2)
=($\frac{5}{9}$+$\frac{4}{9}$)+(-2+1$\frac{5}{6}$)
=1-$\frac{1}{6}$
=$\frac{5}{6}$;
(5)(-$\frac{3}{2}$)+(-$\frac{15}{12}$)+$\frac{5}{2}$+(-$\frac{7}{12}$)
=(-$\frac{3}{2}$+$\frac{5}{2}$)+(-$\frac{15}{12}$-$\frac{7}{12}$)
=1-1
=0;
(6)(-$\frac{1}{3}$)+(+$\frac{2}{5}$)+(+$\frac{3}{5}$)+(-1$\frac{2}{3}$)
=(-$\frac{1}{3}$-1$\frac{2}{3}$)+($\frac{2}{5}$+$\frac{3}{5}$)
=-2+1
=-1.
点评 考查了有理数加法,在进行有理数加法运算时,首先判断两个加数的符号:是同号还是异号,是否有0.从而确定用那一条法则.在应用过程中,要牢记“先符号,后绝对值”.
相关运算律,交换律:a+b=b+a;结合律(a+b)+c=a+(b+c).


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:填空题
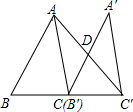 已知:如图,△ABC的面积为12,将△ABC沿BC方向移到△A′B′C′的位置,使B′与C重合,连结AC′交A′C于D,则△C′DC的面积为6.
已知:如图,△ABC的面积为12,将△ABC沿BC方向移到△A′B′C′的位置,使B′与C重合,连结AC′交A′C于D,则△C′DC的面积为6.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 三个数中一定有一个是0 | |
| B. | 三个数若都不为0,则不可能符号都相间 | |
| C. | 一定有两个数互为相反数 | |
| D. | 一定有两个数的和等于第三个数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
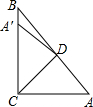 如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠BDA′的度数为( )
如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠BDA′的度数为( )| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com