
分析 根据题中给出的例子找出规律即可得出结论.
解答 解:∵$\frac{1}{\sqrt{2}-1}$=$\sqrt{2}$+1,$\frac{1}{\sqrt{3}-\sqrt{2}}$=$\sqrt{3}$+$\sqrt{2}$,
∴$\frac{1}{\sqrt{n+1}-\sqrt{n}}$=$\sqrt{n+1}$+$\sqrt{n}$(n≥1).
故答案为:$\frac{1}{\sqrt{n+1}-\sqrt{n}}$=$\sqrt{n+1}$+$\sqrt{n}$(n≥1).
点评 本题考查的是分母有理化,熟知分母有理化常常是乘二次根式本身(分母只有一项)或与原分母组成平方差公式是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
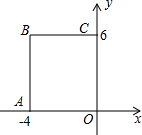 如图,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,A(-4,0),C(0,6),如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{4}$,那么点B的对应点B′的坐标是(-2,3)或(2,-3).
如图,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,A(-4,0),C(0,6),如果矩形OA′B′C′与矩形OABC关于点O位似,且矩形OA′B′C′的面积等于矩形OABC面积的$\frac{1}{4}$,那么点B的对应点B′的坐标是(-2,3)或(2,-3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
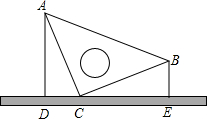 如图,竖直放置一等腰直角三角板,其直角边的长度为10厘米,直角顶点C紧靠在桌面,现量得顶点B到桌面的距离BE=5厘米,则顶点A到桌面的距离AD为( )
如图,竖直放置一等腰直角三角板,其直角边的长度为10厘米,直角顶点C紧靠在桌面,现量得顶点B到桌面的距离BE=5厘米,则顶点A到桌面的距离AD为( )| A. | $5\sqrt{3}$厘米 | B. | $5\sqrt{2}$厘米 | C. | 8厘米 | D. | 6厘米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
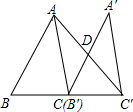 已知:如图,△ABC的面积为12,将△ABC沿BC方向移到△A′B′C′的位置,使B′与C重合,连结AC′交A′C于D,则△C′DC的面积为6.
已知:如图,△ABC的面积为12,将△ABC沿BC方向移到△A′B′C′的位置,使B′与C重合,连结AC′交A′C于D,则△C′DC的面积为6.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
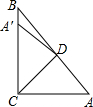 如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠BDA′的度数为( )
如图,在△ABC中,∠ACB=90°,∠A=50°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠BDA′的度数为( )| A. | 40° | B. | 30° | C. | 20° | D. | 10° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com