
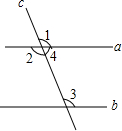
 如图所示,已知直线a、b被直线c所截,以下结论:
如图所示,已知直线a、b被直线c所截,以下结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
科目:初中数学 来源: 题型:选择题
| A. | m=-7,n=-4 | B. | m=-4,n=-4 | C. | m=-4,n=-1 | D. | m=-5,n=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
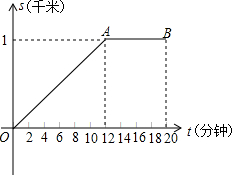 小明早晨从家里出发匀速步行去学校,路上一共用时20分钟.小明的妈妈在小明出发后10分钟,发现小明的数学课本没带,于是她带上课本立即匀速骑车按小明上学的路线追赶小明,结果与小明同时到达学校.设小明从家到学校的过程中,出发t分钟时,他和妈妈所在的位置与家的距离分别为s1(千米)和s2(千米),其中s1(千米)与t(分钟)之间的函数关系的图象为图中的折线段OA-AB.
小明早晨从家里出发匀速步行去学校,路上一共用时20分钟.小明的妈妈在小明出发后10分钟,发现小明的数学课本没带,于是她带上课本立即匀速骑车按小明上学的路线追赶小明,结果与小明同时到达学校.设小明从家到学校的过程中,出发t分钟时,他和妈妈所在的位置与家的距离分别为s1(千米)和s2(千米),其中s1(千米)与t(分钟)之间的函数关系的图象为图中的折线段OA-AB.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由-4x=3,得x=-$\frac{3}{4}$ | B. | 由2x=2,得x=1 | C. | 由2=-3x,得x=-$\frac{3}{2}$ | D. | 由$\frac{1}{2}$x=$\frac{1}{4}$,得x=$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
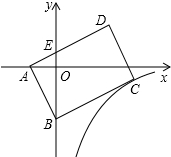 如图,矩形ABCD的顶点A,B的坐标分别是A(-1,0),B(0,-2),反比例函数y=$\frac{k}{x}$的图象经过顶点C,AD边交y轴于点E,若四边形BCDE的面积等于△ABE面积的5倍,则k的值等于-$\frac{3}{2}$.
如图,矩形ABCD的顶点A,B的坐标分别是A(-1,0),B(0,-2),反比例函数y=$\frac{k}{x}$的图象经过顶点C,AD边交y轴于点E,若四边形BCDE的面积等于△ABE面积的5倍,则k的值等于-$\frac{3}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{0.2}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{8}$ | D. | $\sqrt{18}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点D、E分别是△ABC的边AB、AC的中点.点O是△ABC所在平面上的一个动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.
如图,点D、E分别是△ABC的边AB、AC的中点.点O是△ABC所在平面上的一个动点,连接OB、OC,点G、F分别是OB、OC的中点,顺次连接点D、G、F、E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com