
【题目】如图,在正方形ABCD中,E是DC边上一点,(与D、C不重合),连接AE,将△ADE沿AE所在的直线折叠得到△AFE,延长EF交BC于G,连接AG,作GH⊥AG,与AE的延长线交于点H,连接CH.显然AE是∠DAF的平分线,EA是∠DEF的平分线.仔细观察,请逐一找出图中其他的角平分线(仅限于小于180°的角平分线),并说明理由.
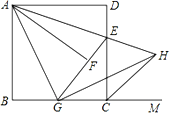
【答案】AG是∠BAF的平分线,GA是∠BGF的平分线;CH是∠DCN的平分线;GH是∠EGM的平分线;理由见解析
【解析】
过点H作HN⊥BM于N,利用正方形的性质及轴对称的性质,证明△ABG≌△AFG,可推出AG是∠BAF的平分线,GA是∠BGF的平分线;证明△ABG≌△GNH,推出HN=CN,得到∠DCH=∠NCH,推出CH是∠DCN的平分线;再证∠HGN=∠EGH,可知GH是∠EGM的平分线.
过点H作HN⊥BM于N,
则∠HNC=90°,
∵四边形ABCD为正方形,
∴AD=AB=BC,∠D=∠DAB=∠B=∠DCB=∠DCM=90°,
①∵将△ADE沿AE所在的直线折叠得到△AFE,
∴△ADE≌△AFE,
∴∠D=∠AFE=∠AFG=90°,AD=AF,∠DAE=∠FAE,
∴AF=AB,
又∵AG=AG,
∴Rt△ABG≌Rt△AFG(HL),
∴∠BAG=∠FAG,∠AGB=∠AGF,
∴AG是∠BAF的平分线,GA是∠BGF的平分线;
②由①知,∠DAE=∠FAE,∠BAG=∠FAG,
又∵∠BAD=90°,
∴∠GAF+∠EAF=![]() ×90°=45°,
×90°=45°,
即∠GAH=45°,
∵GH⊥AG,
∴∠GHA=90°﹣∠GAH=45°,
∴△AGH为等腰直角三角形,
∴AG=GH,
∵∠AGB+∠BAG=90°,∠AGB+∠HGN=90°,
∴∠BAG=∠NGH,
又∵∠B=∠HNG=90°,AG=GH,
∴△ABG≌△GNH(AAS),
∴BG=NH,AB=GN,
∴BC=GN,
∵BC﹣CG=GN﹣CG,
∴BG=CN,
∴CN=HN,
∵∠DCM=90°,
∴∠NCH=∠NHC=![]() ×90°=45°,
×90°=45°,
∴∠DCH=∠DCM﹣∠NCH=45°,
∴∠DCH=∠NCH,
∴CH是∠DCN的平分线;
③∵∠AGB+∠HGN=90°,∠AGF+∠EGH=90°,
由①知,∠AGB=∠AGF,
∴∠HGN=∠EGH,
∴GH是∠EGM的平分线;
综上所述,AG是∠BAF的平分线,GA是∠BGF的平分线,CH是∠DCN的平分线,
GH是∠EGM的平分线.


科目:初中数学 来源: 题型:
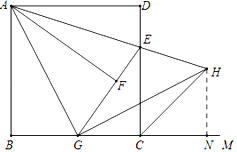
【题目】如图,在△ABC中,∠C=90°,AC=BC,AB=6cm,E是线段AB上一动点,D是BC的中点,过点C作射线CG,使CG∥AB,连接ED,并延长ED交CG于点F,连接AF.设A,E两点间的距离为xcm,A,F两点间的距离为y1cm,E,F两点间的距离为y2cm.小丽根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小丽的探究过程,请补充完整:
(1)按照表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 9.49 | 8.54 | 7.62 | 6.71 | 5.83 | 5.00 | 4.24 |
y2/cm | 9.49 | 7.62 | 5.83 | 3.16 | 3.16 | 4.24 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;

(3)结合函数图象,解决问题:当△AEF为等腰三角形时,AE的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AQ、BN、CN、DQ分別是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AQ与BN相交于点P,CN与DQ相交于点M,判断四边形MNPQ的形状,并证明你的结论.
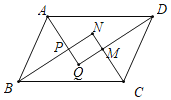
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我市某中学“书香校园”的建设情况,在该校随机抽取了50名学生,调查了解他们一周阅读课外书籍的时间,并将调查结果绘制成如图所示的频数分布直方图(每小组的时间包含最小值,不包含最大值),根据图中信息估计该校1500名学生中,一周课外阅读时间不少于4小时的人数约为( )
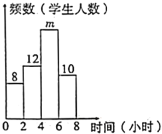
A.300B.600C.900D.1200
查看答案和解析>>
科目:初中数学 来源: 题型:
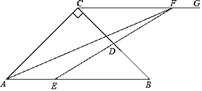
【题目】如图,在△ABC中,AG⊥BC,垂足为点G,点E为边AC上一点,BE=CE,点D为边BC上一点,GD=GB,连接AD交BE于点F.
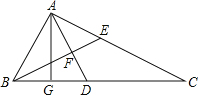
(1)求证:∠ABE=∠EAF;
(2)求证:AE2=EFEC;
(3)若CG=2AG,AD=2AF,BC=5,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织了一次体育测试,测试项目有A“立定跳远”、B“掷实心球”、C“仰卧起坐”、D“100米跑”、E“800米跑”.规定:每名学生测试三项,其中A、B为必测项目,第三项在C、D、E中随机抽取,每项10分(成绩均为整数且不低于0分).
(1)完成A、B必测项目后,用列表法,求甲、乙两同学第三项抽取不同项目的概率;
(2)某班有6名男生抽到了E“800米跑”项目,他们的成绩分别(单位:分)为:x,6,7,8,8,9.
①已知这组成绩的平均数和中位数相等,且x不是这组成绩中最高的,则x= ;
②该班学生丙因病错过了测试,补测抽到了E“800米跑”项目,加上丙同学的成绩后,发现这组成绩的众数与中位数相等,但平均数比原来的平均数小,则丙同学“800米跑”的成绩为多少?;
甲 乙 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是以BC为底的等腰三角形,AD是边BC上的高,点E、F分别是AB、AC的中点.
(1)求证:四边形AEDF是菱形;
(2)如果四边形AEDF的周长为12,两条对角线的和等于7,求四边形AEDF的面积S.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船位于灯塔P的北偏东60°方向,与灯塔P的距离为80海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向的B处,求此时轮船所在的B处与灯塔P的距离.(参考数据:![]() ≈2.449,结果保留整数)
≈2.449,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O在∠APB的平分线上,⊙O与PA相切于点C.
(1)求证:直线PB与⊙O相切;
(2)PO的延长线与⊙O交于点E.若⊙O的半径为3,PC=4.求弦CE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com