
【题目】如图,在△ABC中,∠C=90°,AC=BC,AB=6cm,E是线段AB上一动点,D是BC的中点,过点C作射线CG,使CG∥AB,连接ED,并延长ED交CG于点F,连接AF.设A,E两点间的距离为xcm,A,F两点间的距离为y1cm,E,F两点间的距离为y2cm.小丽根据学习函数的经验,分别对函数y1,y2随自变量x的变化而变化的规律进行了探究.下面是小丽的探究过程,请补充完整:
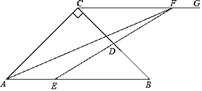
(1)按照表中自变量x的值进行取点、画图、测量,分别得到了y1,y2与x的几组对应值;
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y1/cm | 9.49 | 8.54 | 7.62 | 6.71 | 5.83 | 5.00 | 4.24 |
y2/cm | 9.49 | 7.62 | 5.83 | 3.16 | 3.16 | 4.24 |
(2)在同一平面直角坐标系xOy中,描出补全后的表中各组数值所对应的点(x,y1),(x,y2),并画出函数y1,y2的图象;

(3)结合函数图象,解决问题:当△AEF为等腰三角形时,AE的长度约为 cm.
【答案】(1)4.24;(2)见解析;(3)3.50或5或6.
【解析】
(1)当x=3时,点E是AB的中点,易证△ECF是等腰直角三角形,EF=![]() EC=3
EC=3![]() ≈4.24.
≈4.24.
(2)利用描点法画出函数图象即可解决问题.
(3)由直线y=x与两个函数图象的交点A,B,以及函数y1与函数y2的交点C的横坐标可知,当△AEF为等腰三角形时AE的长度.
解:(1)当x=3时,点E是AB的中点,易证△ECF是等腰直角三角形,EF=![]() EC=3
EC=3![]() ≈4.24.
≈4.24.
(2)函数图象如图所示:
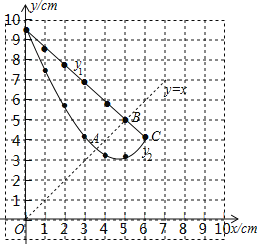
(3)由直线y=x与两个函数图象的交点A,B,以及函数y1与函数y2的交点C的横坐标可知,当△AEF为等腰三角形时,AE的长度约为3.50或5或6.
故答案为3.50或5或6.


 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】时代中学从学生兴趣出发,实施体育活动课走班制.为了了解学生最喜欢的一种球类运动,以便合理安排活动场地,在全校至少喜欢一种球类(乒乓球、羽毛球、排球、篮球、足球)运动的1200名学生中,随机抽取了若干名学生进行调查(每人只能在这五种球类运动中选择一种).调查结果统计如下:
球类名称 | 乒乓球 | 羽毛球 | 排球 | 篮球 | 足球 |
人数 | 42 |
| 15 | 33 |
|
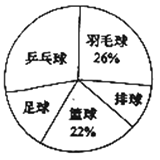
解答下列问题:
(1)这次抽样调查中的样本是________;
(2)统计表中,![]() ________,
________,![]() ________;
________;
(3)试估计上述1200名学生中最喜欢乒乓球运动的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
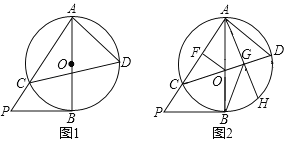
【题目】如图,AB是⊙O的直径,C,D在⊙O上两点,连接AD,CD.
(1)如图1,点P是AC延长线上一点,∠APB=∠ADC,求证:BP与⊙O相切;
(2)如图2,点G在CD上,OF⊥AC于点F,连接AG并延长交⊙O于点H,若CD为⊙O的直径,当∠CGB=∠HGB,BG=2OF=6时,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
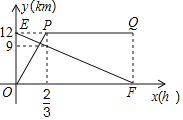
【题目】甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图的折线OPQ和线段EF,分别表示甲、乙两人与A地的距离y甲、y乙与他们所行时间x(h)之间的函数关系.
(1)求线段OP对应的y甲与x的函数关系式并注明自变量x的取值范围;
(2)求y乙与x的函数关系式以及乙到达A地所用的时间;
(3)经过 小时,甲、乙两人相距2km.
查看答案和解析>>
科目:初中数学 来源: 题型:
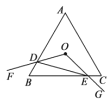
【题目】如图,等边三角形![]() 的边长为4,点
的边长为4,点![]() 是△
是△![]() 的中心,
的中心,![]() .绕点
.绕点![]() 旋转
旋转![]() ,分别交线段
,分别交线段![]() 于
于![]() 两点,连接
两点,连接![]() ,给出下列四个结论:①
,给出下列四个结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 的面积始终等于
的面积始终等于![]() ;④△
;④△![]() 周长的最小值为6,上述结论中正确的个数是( )
周长的最小值为6,上述结论中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青岛市某大酒店豪华间实行淡季、旺季两种价格标准,旺季每间比淡季上涨![]() ,下表是去年该酒店豪华间某两天的相关记录:
,下表是去年该酒店豪华间某两天的相关记录:
旺季 | 淡季 | |
未入住房间数 | 10 | 0 |
日总收入(元) | 24 000 | 40 000 |
(1)该酒店豪华间有多少间?旺季每间价格为多少元
(2)今年旺季来临,豪华间的间数不变。经市场调查发现,如果豪华间仍旧实行去年旺季价格,那么每天都客满;如果价格继续上涨,那么每增加25元,每天未入住房间数增加1间。不考虑其他因素,该酒店将豪华间的价格上涨多少元时,豪华间的日总收入最高?最高日总收入是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.
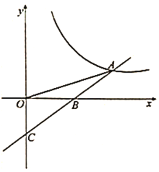
(1)求反比例函数与一次函数的表达式;
(2)若点![]() 为x轴上一点,
为x轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
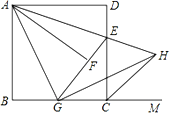
【题目】如图,在正方形ABCD中,E是DC边上一点,(与D、C不重合),连接AE,将△ADE沿AE所在的直线折叠得到△AFE,延长EF交BC于G,连接AG,作GH⊥AG,与AE的延长线交于点H,连接CH.显然AE是∠DAF的平分线,EA是∠DEF的平分线.仔细观察,请逐一找出图中其他的角平分线(仅限于小于180°的角平分线),并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com