
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,点
两点,点![]() 在点
在点![]() 的左侧,抛物线的顶点为
的左侧,抛物线的顶点为![]() ,规定:抛物线与
,规定:抛物线与![]() 轴围成的封闭区域称为“
轴围成的封闭区域称为“![]() 区域”(不包含边界).
区域”(不包含边界).
(1)如果该抛物线经过(1,3),求![]() 的值,并指出此时“
的值,并指出此时“![]() 区域”有_____个整数点;(整数点就是横纵坐标均为整数的点)
区域”有_____个整数点;(整数点就是横纵坐标均为整数的点)
(2)求抛物线![]() 的顶点
的顶点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示);
的代数式表示);
(3)在(2)的条件下,如果![]() 区域中仅有4个整数点时,直接写出
区域中仅有4个整数点时,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)6;(2)顶点![]() 的坐标为
的坐标为![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)将点(1,3)代入抛物线解析式中,即可求出![]() 值,再分别计算当
值,再分别计算当![]() 时,对应的函数值,进而可得在“
时,对应的函数值,进而可得在“![]() 区域”内整数点的坐标,由此可得结论;
区域”内整数点的坐标,由此可得结论;
(2)利用配方法将抛物线的解析式变形为顶点式,由此即可得出顶点![]() 的坐标;
的坐标;
(3)分![]() 及
及![]() 两种情况考虑,依照题意画出图形,结合图形得出关于
两种情况考虑,依照题意画出图形,结合图形得出关于![]() 的不等式组,解之即可得出结论.
的不等式组,解之即可得出结论.
解:(1)∵抛物线![]() 经过(1,3),∴
经过(1,3),∴![]() ,解得:
,解得:![]() .
.
当![]() 时,
时,![]() ,
,![]() ,∴点
,∴点![]() ,点
,点![]() .
.
当![]() 时,
时,![]() ,∴(0,1)、(0,2)两个整数点在“
,∴(0,1)、(0,2)两个整数点在“![]() 区域”;
区域”;
当![]() 时,
时,![]() ,∴(1,1)、(1,2)两个整数点在“
,∴(1,1)、(1,2)两个整数点在“![]() 区域”;
区域”;
当![]() 时,
时,![]() ,∴(2,1)、(2,2)两个整数点在“
,∴(2,1)、(2,2)两个整数点在“![]() 区域”.
区域”.
综上所述:此时“![]() 区域”有6个整数点.
区域”有6个整数点.
故答案为:6.
(2)∵![]() ,∴顶点
,∴顶点![]() 的坐标为
的坐标为![]() .
.
(3)当![]() 时,
时,![]() ,∴抛物线与
,∴抛物线与![]() 轴的交点坐标为
轴的交点坐标为![]() .
.
当![]() 时,如图1所示,此时有
时,如图1所示,此时有![]() ,解得:
,解得:![]() ;
;
当![]() 时,如图2所示,此时有
时,如图2所示,此时有![]() ,解得:
,解得:![]() .
.
综上所述:在(2)的条件下,如果![]() 区域中仅有4个整数点时,则
区域中仅有4个整数点时,则![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于点
的图象交于点![]() ,且与
,且与![]() 轴交于点
轴交于点![]() ;点
;点![]() 在反比例函数
在反比例函数![]() 的图象上,以点
的图象上,以点![]() 为圆心,半径为
为圆心,半径为![]() 的作圆
的作圆![]() 与
与![]() 轴,
轴,![]() 轴分别相切于点
轴分别相切于点![]() 、
、![]() .
.

(1)求反比例函数和一次函数的解析式;
(2)请连结![]() ,并求出
,并求出![]() 的面积;
的面积;
(3)直接写出当![]() 时,
时,![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某足球特色学校在商场购买甲、乙两种品牌的足球.已知乙种足球比甲种足球每只贵20元,该校分别花费2000元、1400元购买甲、乙两种足球,这样购得甲种足球的数量是购得乙种足球数量的2倍,求甲、乙两种足球的单价各是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学完二元一次方程组的应用之后,老师写出了一个方程组如下:![]() ,要求把这个方程组赋予实际情境.
,要求把这个方程组赋予实际情境.
小军说出了一个情境:学校有两个课外小组,书法组和美术组,其中书法组的人数的二倍比美术组多5人,书法组平均每人完成了4幅书法作品,美术组平均每人完成了3幅美术作品,两个小组共完成了40幅作品,问书法组和美术组各有多少人?
小明通过验证后发现小军赋予的情境有问题,请找出问题在哪?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“已知底边及底边上的高线作等腰三角形”的尺规作图过程.
已知:线段![]() .求作:等腰
.求作:等腰![]() ,使
,使![]() ,
,![]() 边上的高为
边上的高为![]() .作法:如图,(1)作线段
.作法:如图,(1)作线段![]() ;(2)作线段
;(2)作线段![]() 的垂直平分线
的垂直平分线![]() 交
交![]() 于点
于点![]() ;(3)在射线
;(3)在射线![]() 上顺次截取线段
上顺次截取线段![]() ,连接
,连接![]() .所以
.所以![]() 即为所求作的等腰三角形.
即为所求作的等腰三角形.
请回答:得到![]() 是等腰三角形的依据是:
是等腰三角形的依据是:
①_____:
②_____.
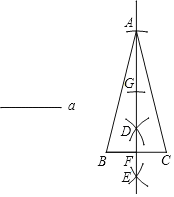
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的变换点
的变换点![]() 的坐标定义如下:
的坐标定义如下:
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ;当
;当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() .
.
(1)点![]() 的变换点
的变换点![]() 的坐标是 ;点
的坐标是 ;点![]() 的变换点为
的变换点为![]() ,连接
,连接![]() ,则
,则![]() °;
°;
(2)已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() (点
(点![]() 在点
在点![]() 的左侧),顶点为
的左侧),顶点为![]() .点
.点![]() 在抛物线
在抛物线上,点
![]() 的变换点为
的变换点为![]() .若点
.若点![]() 恰好在抛物线的对称轴上,且四边形
恰好在抛物线的对称轴上,且四边形![]() 是菱形,求
是菱形,求![]() 的值;
的值;
(3)若点![]() 是函数
是函数![]() 图象上的一点,点
图象上的一点,点![]() 的变换点为
的变换点为![]() ,连接
,连接![]() ,以
,以![]() 为直径作
为直径作![]() ,
,![]() 的半径为
的半径为![]() ,请直接写出
,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系中有两点A(0,1),B(﹣1,0),动点P在反比例函数y=![]() 的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为_____.
的图象上运动,当线段PA与线段PB之差的绝对值最大时,点P的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对于点P(x,y),如果点Q(x,y′)的纵坐标满足y′=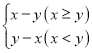 ,那么称点Q为点P的“关联点”.
,那么称点Q为点P的“关联点”.
(1)请直接写出点(3,5)的“关联点”的坐标 ;
(2)如果点P在函数y=x﹣2的图象上,其“关联点”Q与点P重合,求点P的坐标;
(3)如果点M(m,n)的“关联点”N在函数y=2x2的图象上,当0≤m≤2时,求线段MN的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com