练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．已知方程4x+2m=3x+1和方程3x+2m=6x+1的解相同，求：
    （1）m的值；
    （2）代数式（m+2）（2m-$\frac{7}{5}$）的值．

    分析 （1）根据同解方程，可得方程组，根据解方程组，可得答案；
    （2）根据代数式求值，可得答案．

    解答 解：（1）方程4x+2m=3x+1和方程3x+2m=6x+1的解相同，得
    $\left\{\begin{array}{l}{4x+2m=3x+1①}\\{3x+2m=6x+1②}\end{array}\right.$，
    解得$\left\{\begin{array}{l}{x=0}\\{m=\frac{1}{2}}\end{array}\right.$，
    m的值是$\frac{1}{2}$；
    （2）当m=$\frac{1}{2}$时，（m+2）（2m-$\frac{7}{5}$）=（$\frac{1}{2}$+2）（2×$\frac{1}{2}$-$\frac{7}{5}$）
    =$\frac{5}{2}$×（-$\frac{2}{5}$）=-1．

    点评 本题考查了同解方程，利用同解方程得出方程组是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    11．如果a、b互为倒数，c、d互为相反数，且m是绝对值最小的有理数，则代数式2ab-（c+d）+m2的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．已知：二次函数y=x2-2x-3．
    （1）运用对称性，画出这个二次函数图象；
    （2）当x满足条件x＜-1或x＞2条件时，y≥0，不等式-x2+2x+3＞0的解集为-1＜x＜3；
    （3）当-1＜x＜4时，求y的取值范围是-4≤y＜5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

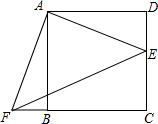    9．如图，点E是正方形ABCD的边DC上一点，把△ADE顺时针旋转至△ABF的位置．
    （1）旋转中心是点A，旋转角度是90度；
    （2）若连结EF，则△AEF是等腰直角三角形；并证明；
    （3）若四边形AECF的面积为36，DE=2，求EF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

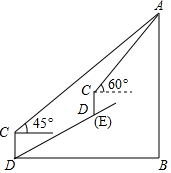    16．如图，在一次数学课外实践活动中，要求测量山坡前某建筑物的高度 AB．小刚在D处用高1.5m的测角仪CD，测得该建筑物顶端A的仰角为45°，然后沿倾斜角为30°的山坡向上前进20m到达E，重新安装好测角仪CD后又测得该建筑物顶端A的仰角为60°．求该建筑物的高度AB．（结果保留根号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．计算
    （1）$\frac{\sqrt{3}tan30°}{2tan45°-1}$                
    （2）$\sqrt{27}$-6sin60°+（π-3.14）0+|-$\sqrt{5}$|

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．10袋小麦，如果以40千克为准，超过的千克数记作正数，不足的千克数记做负数．称重的纪录如下：
    +2，+1，-0.5，-1，-2，+3，-0.5，-1，-1，0
    （1）这10袋小麦中，最轻是多少千克？最重是多少千克？直接回答
    （2）这10袋小麦的总重量是多少千克？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如图，⊙O中，直径AB⊥弦CD于点E，弦CG=CD，且交半径OB于点F，射线DG交AB的延长线于点H，若OE=$\frac{4}{3}$，OH=6，则CD=$\frac{4}{3}$$\sqrt{22}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图所示，有三条公路L1，L2，L3两两相交，若选择一地点建座加油站，使它到三条公路的距离都相等．应如何选择加油站的地址？这样的地址有几处？

    查看答案和解析>>

    同步练习册答案