
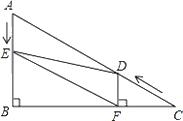
【题目】如图,在Rt△ABC中,∠B=90°,BC=5![]() ,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
,∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒(t>0).过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
(3)当t为何值时,△DEF为直角三角形?请说明理由.
【答案】(1)证明见解析;(2)能,![]() ;(3)
;(3)![]() 或4时,△DEF为直角三角形.
或4时,△DEF为直角三角形.
【解析】
![]() 在
在![]() 中,
中,![]() ,
,![]() ,根据30°角直角三角形的性质及已知条件即可证得结论;
,根据30°角直角三角形的性质及已知条件即可证得结论;
![]() 先证得四边形AEFD为平行四边形,使AEFD为菱形则需要满足的条件为AE=AD,由此即可解答;
先证得四边形AEFD为平行四边形,使AEFD为菱形则需要满足的条件为AE=AD,由此即可解答;
![]() 时,四边形EBFD为矩形
时,四边形EBFD为矩形![]() 在Rt△AED中求可得
在Rt△AED中求可得![]() ,由此即可解答;
,由此即可解答;![]() 时,由
时,由![]() 知
知![]() ,则得
,则得![]() ,求得
,求得![]() ,由此列方程求解即可;
,由此列方程求解即可;![]() 时,此种情况不存在.
时,此种情况不存在.
![]() 在
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
![]() 能,
能,
![]() ,
,![]() ,
,
![]() .
.
又![]() ,
,
![]() 四边形AEFD为平行四边形.
四边形AEFD为平行四边形.
![]() ,
,
![]() .
.
![]() .
.
若使AEFD为菱形,则需![]() ,
,
即![]() ,
,![]() .
.
即当![]() 时,四边形AEFD为菱形.
时,四边形AEFD为菱形.
![]()
![]() 时,四边形EBFD为矩形.
时,四边形EBFD为矩形.
在![]() 中,
中,![]() ,
,
![]() .
.
即![]() ,
,![]() .
.
![]() 时,由
时,由![]() 四边形AEFD为平行四边形知
四边形AEFD为平行四边形知![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
即![]() ,
,![]() .
.
![]() 时,此种情况不存在.
时,此种情况不存在.
综上所述,当![]() 秒或4秒时,
秒或4秒时,![]() 为直角三角形.
为直角三角形.


科目:初中数学 来源: 题型:
【题目】将正面分别标有数字2,3,4的三张形状、大小一样的卡片洗匀后,背面朝上放在桌面上.
(1)随机地抽取一张卡片,求抽到奇数的概率;
(2)随机地抽取一张卡片,将卡片上标有的数字作为十位上的数字(不放回),再随机地抽取一张卡片,将卡片上标有的数字作为个位上的数字,组成的两位数恰好是“23”的概率是多少?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某武警部队在一次地震抢险救灾行动中,探险队员在相距4米的水平地面A,B两处均探测出建筑物下方C处有生命迹象,已知在A处测得探测线与地面的夹角为30°,在B处测得探测线与地面的夹角为60°,求该生命迹象C处与地面的距离.(结果精确到0.1米,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
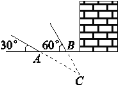
查看答案和解析>>
科目:初中数学 来源: 题型:
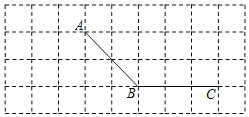
【题目】如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.
![]() 过点C画线段AB的平行线CD;
过点C画线段AB的平行线CD;
![]() 过点A画线段BC的垂线,垂足为E;
过点A画线段BC的垂线,垂足为E;
![]() 过点A画线段AB的垂线,交线段CB的延长线于点F;
过点A画线段AB的垂线,交线段CB的延长线于点F;
![]() 线段AE的长度是点______到直线______的距离;
线段AE的长度是点______到直线______的距离;
![]() 线段AE、BF、AF的大小关系是______
线段AE、BF、AF的大小关系是______![]() 用“
用“![]() ”连接
”连接![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
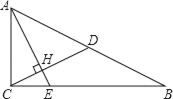
【题目】如图,已知Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,过点A作AE⊥CD,AE分别与CD、CB相交于点H、E,AH=2CH.
(1)求sinB的值;
(2)如果CD=![]() ,求BE的值.
,求BE的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com