
����Ŀ��С���ľߵ����7�·ݹ���һ���ʼDZ�����2290����ÿ������Ϊ10Ԫ�����ľߵ������8�·ݿ�ʼ�������ۣ���ÿ���ۼ�Ϊ11Ԫ�����ȫ�����ꣻ��ÿ���ۼ�ÿ����1Ԫ�������ͼ���30����
��1�������ֱʼDZ���8�·ݵ�������������2200������8�·��ۼ�Ӧ�����ڶ���Ԫ��
��2�����������������ֽ���գ��ñʼDZ��Ľ��������10%���ľߵ�Ϊ�����ӱʼDZ����������������۵������ۼ۱�8�·��ڣ�1���������µ�����ۼۼ�����![]() m%�����9�·ݵ�������8�·��ڣ�1���������µ��������������m%��9�·ݵ���������ﵽ6600Ԫ����m��ֵ��
m%�����9�·ݵ�������8�·��ڣ�1���������µ��������������m%��9�·ݵ���������ﵽ6600Ԫ����m��ֵ��
���𰸡���1��8�·��ۼ�Ӧ������14Ԫ����2��m��ֵ��50��
��������
��1����8�·��ۼ�ӦΪxԪ�����ݲ��ȹ�ϵ�����ֱʼDZ���8�·ݵ�������������2200�����г�����ʽ��⼴�ɣ�
��2�������9�·ݵĽ������ۼۣ��ٸ��ݵ�����ϵ��9�·ݵ���������ﵽ6600Ԫ���г�������⼴�ɣ�
�⣺��1����8�·��ۼ�ӦΪxԪ��������ã�
2290��30��x��11����2200��
���x��14��
��8�·��ۼ�Ӧ������14Ԫ��
��2��9�·ݵĽ���Ϊ10��1+10%��=11Ԫ���ۼ�Ϊ14��1��![]() m%��Ԫ���������⣬��
m%��Ԫ���������⣬��
![]()
��m%��t����ԭ���̿ɻ�Ϊ��3��2t����1+t����3��
���t1��0���������⣬��ȥ����t2��0.5��
��m��50��
��m��ֵ��50��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУҪ�ٰ�һ���ݽ�������ÿ��ֻ��ѡһ�˲μӱ����������꼶һ��мס������˵��ݽ�ˮƽ������£���Ҫ������������ѡһ��ȥ�μ�ȫУ���ݽ�����������������ȫ��ͬѧЭ�̾�������С�����Ϸ��ȷ��˭ȥ������ʤ�߲�������
��Ϸ�������£������������ĺ����У�һ�������������������һ��������һ�������������������һ���������������и���һ���������õ��������Ǻ���ʤ�����õ��������ǰ�����ʤ��������Ϊƽ�֣���Ϊƽ�֣�����������Ϸ��ֱ���ֳ�ʤ��Ϊֹ��
������������ش��������⣺
��1�����������Ӹ�����һ����һ����Ϊ����һ����Ϊ����ĸ����Ƕ��٣�
��2������Ϸ��ƽ�������б�����״ͼ�ȷ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ڵȱߡ�ABC�У�CDΪ���ߣ���Q���߶�CD���˶������߶�QA�Ƶ�Q˳ʱ����ת��ʹ�õ�A�Ķ�Ӧ��E��������BC�ϣ�����BQ�����DAQ=����0��������60��������30������
��1����0��������30��ʱ��
����ͼ1�������⻭��ͼ�Σ������BQE���ú�����ʽ�ӱ�ʾ����
��̽���߶�CE��AC��CQ֮���������ϵ��������֤����
��2����30��������60��ʱ��ֱ��д���߶�CE��AC��CQ֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
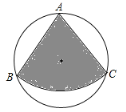
����Ŀ����ͼ����һ��뾶Ϊ![]() ��Բ����Ƥ�ϼ���һ��Բ�Ľ���
��Բ����Ƥ�ϼ���һ��Բ�Ľ���![]() ������
������![]() ���������Χ�ɵ�Բ�IJ����Ϊ�� ��
���������Χ�ɵ�Բ�IJ����Ϊ�� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
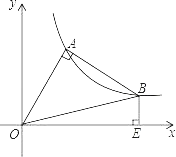
����Ŀ����OAB�ڵ�һ�����У�OA��AB��OA��AB��O������ԭ�㣬�Һ���y��![]() ���ù�A��B���㣬BE��x����E�㣬��OE2��BE2��ֵΪ��������
���ù�A��B���㣬BE��x����E�㣬��OE2��BE2��ֵΪ��������
A. 3B. 2C. 3D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����л�����ʡ��̫ԭ��һ����ںӴ���(��ͼ1)����������߶Ȳ�ͬ���羶Ҳ��ͬ���������ֹ�ͨ�����ţ�������������������ߵĸֹ���ͼ2��ʾ���˸ֹ�(���ƿ��ɶ��κ�����ͼ��-������)��ͬһ��ֱƽ���ڣ��빰�����ڵ�ˮƽ���ཻ��A��B���㣬����Ϊ78��(����ߵ�O��AB�ľ���Ϊ78��)���羶Ϊ90��(��AB=90��)������ߵ�OΪ����ԭ�㣬��ƽ����AB��ֱ��Ϊ![]() �Ὠ��ƽ��ֱ������ϵ����������߸ֹ��ĺ�������ʽΪ( )
�Ὠ��ƽ��ֱ������ϵ����������߸ֹ��ĺ�������ʽΪ( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���о�������һ�������⣺��ͼ 1����ABC �У��� AB �� A ˳ʱ����ת 00 1800 �õ� AB ���� AC �Ƶ� A ��ʱ����ת �õ� AC ������ BC ���� 180�� ʱ�� ����ABC �� BC �ϵ����� AD �� BC ��������ϵ��ʲô�� �����������о����̣�

������֤��
��1������ͼ 2����ABC Ϊ�ȱ�������ʱ��AD �� BC ��������ϵΪ AD ����BC ��
����ͼ 3����BAC 900 , BC 8ʱ���� AD ��Ϊ ��������
������֤��
��2����ͼ 1 �У���ABC Ϊ����������ʱ������ AD �� BC ��������ϵ��������֤����
��չӦ��
��3����ͼ 4�����ı��� ABCD ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �����ı����ڲ��Ƿ���ڵ� P ��ʹPDC ��PAB ֮������С��̽���������еı߽ǹ�ϵ�������ڣ� �뻭���� P ��λ�ã�������ͼ�ۼ�������Ҫ˵������ֱ��д��PDC �ı� DC �ϵ����� PQ �ij��ȣ��������ڣ�˵�����ɣ�
�����ı����ڲ��Ƿ���ڵ� P ��ʹPDC ��PAB ֮������С��̽���������еı߽ǹ�ϵ�������ڣ� �뻭���� P ��λ�ã�������ͼ�ۼ�������Ҫ˵������ֱ��д��PDC �ı� DC �ϵ����� PQ �ij��ȣ��������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ����ë�����У����˶�Ա�������![]() ��P�㴦��������˶��켣PAN����һ�������ߵ�һ���֣������˶�����ߵ�Aʱ����߶�Ϊ3�ף�����˶�Ավ���ص�O��ˮƽ����Ϊ5�ף�����BC���O��ˮƽ����Ϊ6�ף��Ե�OΪԭ�㽨����ͼ��ʾ������ϵ�����˶�Ավ���ص�M������Ϊ��m��0��.
��P�㴦��������˶��켣PAN����һ�������ߵ�һ���֣������˶�����ߵ�Aʱ����߶�Ϊ3�ף�����˶�Ավ���ص�O��ˮƽ����Ϊ5�ף�����BC���O��ˮƽ����Ϊ6�ף��Ե�OΪԭ�㽨����ͼ��ʾ������ϵ�����˶�Ավ���ص�M������Ϊ��m��0��.

��1���������ߵĽ���ʽ����Ҫ��д�Ա�����ȡֵ��Χ����
��2������ë����ص�N��������ˮƽ���루��NC�ij�����
��3����ԭ��������ɽ�������߶�Ϊ2.4�ף�������Ϊ����߶Ȳ�����ʧ����m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ����һ��֪ʶ���������������4С�⣬ÿС��5�֣���Ը�5�֣�������0�֣��ڸ�ѧУ�����ȡ����ͬѧ�μӱ������ɼ����Ƴɲ�������ͳ�Ʊ����£�
�ɼ� | ������Ƶ���� | �ٷֱȣ�Ƶ�ʣ� |
0 | ||
5 | 0.2 | |
10 | 5 | |
15 | 0.4 | |
20 | 5 | 0.1 |
���ݱ������е���Ϣ�����н�����ȷ���ǣ�������
A. ����40��ͬѧ�μ�֪ʶ����
B. �鵽��ͬѧ�μ�֪ʶ������ƽ���ɼ�Ϊ10��
C. ��֪��У����800��ѧ���������μӾ�������0�ֵĹ�����100��
D. �鵽ͬѧ�μ�֪ʶ�����ɼ�����λ��Ϊ15��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com