
【题目】如图,从一块半径为![]() 的圆形铁皮上剪出一个圆心角是
的圆形铁皮上剪出一个圆心角是![]() 的扇形
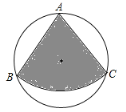
的扇形![]() ,则此扇形围成的圆锥的侧面积为( )
,则此扇形围成的圆锥的侧面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
连接OB、OC和BC,过点O作OD⊥BC于点D,然后根据同弧所对的圆周角是圆心角的一半、等边三角形判定和垂径定理可得∠BOC=2∠BAC=120°,△ABC为等边三角形,BC=2BD,然后根据锐角三角函数即可求出BD,从而求出BC和AB,然后根据扇形的面积公式计算即可.
解:连接OB、OC和BC,过点O作OD⊥BC于点D

由题意可得:OB=OC=20cm,∠BAC=60°,AB=AC
∴∠BOC=2∠BAC=120°,△ABC为等边三角形,BC=2BD
∴∠OBC=∠OCB=![]() (180°-∠BOC)=30°,AB=AC=BC
(180°-∠BOC)=30°,AB=AC=BC
在Rt△OBD中,BD=OB·cos∠OBD=![]() cm
cm
∴BC=2BD=![]() cm
cm
∴AB=BC=![]() cm
cm
∴圆锥的侧面积=S扇形BAC=![]()
故选A.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AC=6,BC=8,AB=10,以点C为圆心,4为半径作圆.点D是⊙C上的一个动点,连接AD、BD,则AD+![]() BD的最小值为__________.
BD的最小值为__________.
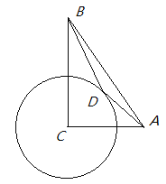
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系 xOy 中,抛物线 y mx![]() 2mx 3与 y 轴交于点C ,该抛物线对称轴与 x 轴的交于点 A.
2mx 3与 y 轴交于点C ,该抛物线对称轴与 x 轴的交于点 A.
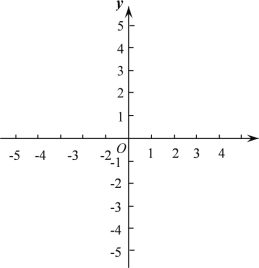
(1)求该抛物线的对称轴及点 A 、C 的坐标;
(2)点 A 向右移动两个单位长度,向上移动两个单位长度,得到点 B,若抛物线与线段 AB恰有一个交点时,结合图象,求 m 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
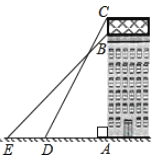
【题目】如图,一座商场大楼的顶部竖直立有一个矩形广告牌,小红同学在地面上选择了在条直线上的三点![]() 为楼底),
为楼底),![]() ,她在
,她在![]() 处测得广告牌顶端
处测得广告牌顶端![]() 的仰角为
的仰角为![]() ,在
,在![]() 处测得商场大楼楼顶
处测得商场大楼楼顶![]() 的仰角为
的仰角为![]()
![]() 米.已知广告牌的高度
米.已知广告牌的高度![]() 米,求这座商场大楼的高度
米,求这座商场大楼的高度![]() (
(![]() ,小红的身高不计,结果保留整数).
,小红的身高不计,结果保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,完成(1),(2)两题
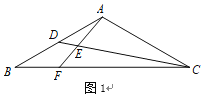
数学课上,老师出示了这样一道题:如图1,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 上一点,且满足
上一点,且满足![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() ,延长
,延长![]() 交
交![]() 于
于![]() ,求
,求![]() 的值.同学们经过思考后,交流了自己的想法:
的值.同学们经过思考后,交流了自己的想法:
小明:“通过观察和度量,发现![]() 与
与![]() 相等.”
相等.”
小伟:“通过构造全等三角形,经过进一步推理,就可以求出![]() 的值.”
的值.”
……
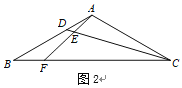
老师:“把原题条件中的‘![]() ’,改为‘
’,改为‘![]() ’其他条件不变(如图2),也可以求出
’其他条件不变(如图2),也可以求出![]() 的值.
的值.
(1)在图1中,①求证:![]() ;②求出
;②求出![]() 的值;
的值;
(2)如图2,若![]() ,直接写出
,直接写出![]() 的值(用含
的值(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小飞文具店今年7月份购进一批笔记本,共2290本,每本进价为10元,该文具店决定从8月份开始进行销售,若每本售价为11元,则可全部售完;且每本售价每增长1元,销量就减少30本.
(1)若该种笔记本在8月份的销售量不低于2200本,则8月份售价应不高于多少元?
(2)由于生产商提高造纸工艺,该笔记本的进价提高了10%,文具店为了增加笔记本的销量进行了销售调整,售价比8月份在(1)的条件下的最高售价减少了![]() m%,结果9月份的销量比8月份在(1)的条件下的最低销量增加了m%,9月份的销售利润达到6600元,求m的值.
m%,结果9月份的销量比8月份在(1)的条件下的最低销量增加了m%,9月份的销售利润达到6600元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解七年级学生体育测试情况,在七年级各班随机抽取了部分学生的体育测试成绩,按![]() 四个等级进行统计(说明:
四个等级进行统计(说明:![]() 级:90分~100分;
级:90分~100分;![]() 级:75分~89分;
级:75分~89分;![]() 级:60分~74分;
级:60分~74分;![]() 级:60分以下),并将统计结果绘制成两个不完整的统计图,请你结合统计图中所给信息解答下列问题:
级:60分以下),并将统计结果绘制成两个不完整的统计图,请你结合统计图中所给信息解答下列问题:
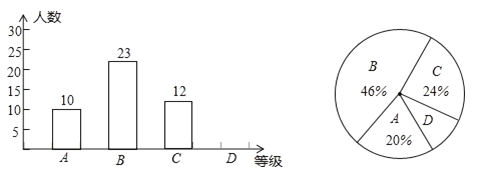
(1)学校在七年级各班共随机调查了________名学生;
(2)在扇形统计图中,![]() 级所在的扇形圆心角的度数是_________;
级所在的扇形圆心角的度数是_________;
(3)请把条形统计图补充完整;
(4)若该校七年级有500名学生,请根据统计结果估计全校七年级体育测试中![]() 级学生约有多少名?
级学生约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(-1,1)且经过点B,连接AB,直线AB与此抛物线的另一个交点为C,则S△BCD:S△ABO=( )

A. 8:1B. 6:1C. 5:1D. 4:1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com