
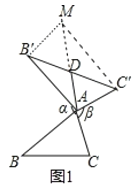
����Ŀ��С���о�������һ�������⣺��ͼ 1����ABC �У��� AB �� A ˳ʱ����ת 00 1800 �õ� AB ���� AC �Ƶ� A ��ʱ����ת �õ� AC ������ BC ���� 180�� ʱ�� ����ABC �� BC �ϵ����� AD �� BC ��������ϵ��ʲô�� �����������о����̣�

������֤��
��1������ͼ 2����ABC Ϊ�ȱ�������ʱ��AD �� BC ��������ϵΪ AD ����BC ��
����ͼ 3����BAC 900 , BC 8ʱ���� AD ��Ϊ ��������
������֤��
��2����ͼ 1 �У���ABC Ϊ����������ʱ������ AD �� BC ��������ϵ��������֤����
��չӦ��
��3����ͼ 4�����ı��� ABCD ��![]() ��
��![]() ��
��![]() ��
��![]() ��
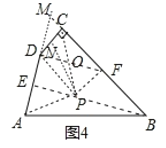
��![]() �����ı����ڲ��Ƿ���ڵ� P ��ʹPDC ��PAB ֮������С��̽���������еı߽ǹ�ϵ�������ڣ� �뻭���� P ��λ�ã�������ͼ�ۼ�������Ҫ˵������ֱ��д��PDC �ı� DC �ϵ����� PQ �ij��ȣ��������ڣ�˵�����ɣ�
�����ı����ڲ��Ƿ���ڵ� P ��ʹPDC ��PAB ֮������С��̽���������еı߽ǹ�ϵ�������ڣ� �뻭���� P ��λ�ã�������ͼ�ۼ�������Ҫ˵������ֱ��д��PDC �ı� DC �ϵ����� PQ �ij��ȣ��������ڣ�˵�����ɣ�
���𰸡���1����![]() ��4 ��2��
��4 ��2��![]() ��֤�������� ��3�����ڣ���ͼ��������
��֤�������� ��3�����ڣ���ͼ��������![]()
��������
��1��������֤��![]() �Ǻ���30����ֱ�������Σ��ɵ�
�Ǻ���30����ֱ�������Σ��ɵ�![]() �����ɽ�����⣻������֤��
�����ɽ�����⣻������֤��![]() ������ֱ��������б�����߶������ɽ�����⣻
������ֱ��������б�����߶������ɽ�����⣻
��2�����ۣ�![]() ���ӳ�AD��M��ʹ��
���ӳ�AD��M��ʹ��![]() ������
������![]() ����֤���ı���
����֤���ı���![]() ��ƽ���ı��Σ���֤��
��ƽ���ı��Σ���֤��![]() �����ɽ�����⣻
�����ɽ�����⣻
��3�����ڣ���ͼ4���ӳ�AD��BC���ӳ�����M����![]() ��E�����߶�BC�Ĵ�ֱƽ���߽�BE��P����BC��F������PA��PD��PC������PCD������PN������DF��PC��O����֤��
��E�����߶�BC�Ĵ�ֱƽ���߽�BE��P����BC��F������PA��PD��PC������PCD������PN������DF��PC��O����֤��![]() ����֤��
����֤��![]() �����ɵó����ۣ��ٸ��ݹ��ɶ������PC�ij����������PQ�ij���
�����ɵó����ۣ��ٸ��ݹ��ɶ������PC�ij����������PQ�ij���
��1���١ߡ�ABC�ǵȱ�������
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
�ʴ�Ϊ��![]()
�ڡ�![]()
��![]()
��![]()
��![]()
��![]()
��![]()
�ʴ�Ϊ��4��
��2��![]()
��ͼ��1���У��ӳ�AD��M��ʹ��![]() ������
������![]()
��![]()
���ı���![]() ��ƽ���ı���
��ƽ���ı���
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��![]() ��
��
��3�����ڣ���ͼ4���ӳ�AD��BC���ӳ�����M����![]() ��E�����߶�BC�Ĵ�ֱƽ���߽�BE��P����BC��F������PA��PD��PC������PCD������PN������DF��PC��O
��E�����߶�BC�Ĵ�ֱƽ���߽�BE��P����BC��F������PA��PD��PC������PCD������PN������DF��PC��O
��![]()
��![]()
��![]()
��![]()
��Rr��DCM��
��![]()
��![]()
��Rt��BEM��
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
��![]() ��
��![]()
��Rt��CDF��
��![]()
��![]()
��![]()
��![]()
��![]()
��![]()
���ı���CDPF�Ǿ���
��![]()
��![]()
���ADP�ǵȱ�������
��![]()
��![]()
��![]()
��![]()
���ɣ�1�����۵�![]()
��PDC ��PAB ֮������С��̽���������еı߽ǹ�ϵ
��Rt��FCP��
��![]()
��![]()
��![]() ��
��


 �Ͻ�ƽ���Ȿϵ�д�
�Ͻ�ƽ���Ȿϵ�д� ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
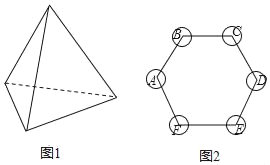
����Ŀ��ͼ����һö�ʵؾ��ȵ�����������״�����ӣ�ÿ�����Ϸֱ��������2��3��4��5��ͼ����һ�������������̣���ͨ�������ӵķ�ʽ��������Ϸ�������ǣ�����ö�����������������������������ϣ������棩�������Ǽ����ʹ�ͼ�е�A�㿪ʼ����˳ʱ�뷽�����������������㣬�ڶ��δӵ�һ�ε��յ㴦��ʼ������һ�εķ�����������
��1�������һ�����ӣ���������������C���ĸ������� ����
��2��������������ӣ��û���״ͼ���б��ķ�����������������������C���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��ͼ����
��ͼ����![]() �ύ�ڵ�
�ύ�ڵ�![]() �͵�
�͵�![]() ,��
,��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��ֱ��
��ֱ��![]() ���������ڵ�
���������ڵ�![]() �͵�
�͵�![]() ������
������![]() ��
��
![]() ��
��![]() �����꣮
�����꣮
![]() ��
��![]() �������
�������
![]() ֱ��д����
ֱ��д����![]() ʱ���Ա���
ʱ���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ľߵ����7�·ݹ���һ���ʼDZ�����2290����ÿ������Ϊ10Ԫ�����ľߵ������8�·ݿ�ʼ�������ۣ���ÿ���ۼ�Ϊ11Ԫ�����ȫ�����ꣻ��ÿ���ۼ�ÿ����1Ԫ�������ͼ���30����
��1�������ֱʼDZ���8�·ݵ�������������2200������8�·��ۼ�Ӧ�����ڶ���Ԫ��
��2�����������������ֽ���գ��ñʼDZ��Ľ��������10%���ľߵ�Ϊ�����ӱʼDZ����������������۵������ۼ۱�8�·��ڣ�1���������µ�����ۼۼ�����![]() m%�����9�·ݵ�������8�·��ڣ�1���������µ��������������m%��9�·ݵ���������ﵽ6600Ԫ����m��ֵ��
m%�����9�·ݵ�������8�·��ڣ�1���������µ��������������m%��9�·ݵ���������ﵽ6600Ԫ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����²��ϣ�����Ҫ�������Ӧ������
����������ŷ����Leonhard Euler������ʿ��ѧ�ң�����ѧ�Ͼ�������������������������Ҫ��������ʽ�Ͷ�����������ŷ�����ֵ�һ������������ABC �У�R �� r �ֱ�Ϊ���Բ������Բ�İ뾶��O �� I �ֱ�Ϊ�����ĺ����ģ���OI ![]() R
R![]() 2Rr .
2Rr .
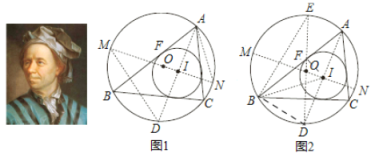
�����Ǹö�����֤�����̣������˵�(2)�ʵĽ��ۣ���
�ӳ�AI ����O �ڵ� D������ I ����O ��ֱ�� MN������ DM��AN.
�ߡ�D=��N�����DMI=��NAI��ͬ�����Ե�Բ�ܽ���ȣ���
���MDI�ס�ANI.��![]() ���� IA ID IM IN ��
���� IA ID IM IN ��
��ͼ�ڣ���ͼ 1����ȥ MD��AN���Ļ���������O ��ֱ��DE������BE��BD��BI��IF
��DE �ǡ�O ��ֱ�������DBE=90��.
�ߡ�I �� AB �����ڵ� F�����AFI=90����
���DBE=��IFA.
�ߡ�BAD=��E��ͬ������Բ�ܽ���ȣ���
���AIF�ס�EDB��
��![]() ����
����![]() �ڣ�
�ڣ�
�ɣ�2��֪��![]() ��
��
��![]()
�֡�![]() ��
��
�� 2Rr(R d )(R d ) ��
�� R![]() d
d![]() 2Rr
2Rr
�� d ![]() R
R![]() 2Rr
2Rr
����1���۲췢�֣� IM R d �� IN ���ú�R��d �Ĵ���ʽ��ʾ����
��2�����ж� BD �� ID ��������ϵ����˵������.��������ͼ 1 ֤����
��3��Ӧ�ã�����ABC �����Բ�İ뾶Ϊ 6cm������Բ�İ뾶Ϊ 2cm������ABC ������������֮��ľ���Ϊ ����cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽����꼶ѧ��������������������꼶���������ȡ�˲���ѧ�����������Գɼ�����![]() �ĸ��ȼ�����ͳ��(˵����
�ĸ��ȼ�����ͳ��(˵����![]() ����90�֡�100�֣�
����90�֡�100�֣�![]() ����75�֡�89�֣�
����75�֡�89�֣�![]() ����60�֡�74�֣�
����60�֡�74�֣�![]() ����60������)������ͳ�ƽ�����Ƴ�������������ͳ��ͼ��������ͳ��ͼ��������Ϣ����������⣺
����60������)������ͳ�ƽ�����Ƴ�������������ͳ��ͼ��������ͳ��ͼ��������Ϣ����������⣺
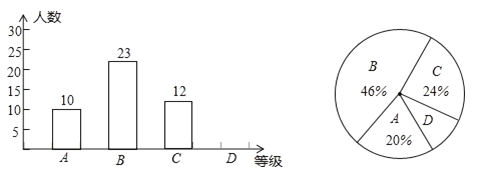
��1��ѧУ�����꼶������������________��ѧ����
��2��������ͳ��ͼ�У�![]() �����ڵ�����Բ�ĽǵĶ�����_________��
�����ڵ�����Բ�ĽǵĶ�����_________��
��3���������ͳ��ͼ����������
��4������У���꼶��500��ѧ���������ͳ�ƽ������ȫУ���꼶����������![]() ��ѧ��Լ�ж�������
��ѧ��Լ�ж�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У��Ƚ�������y��2x2��4x����y������ԳƱ任���ٽ����õ������ߣ������Ķ�����ת180������ô�����α任�����õ��������ߵĺ�������ʽΪ��������
A.y����2x![]() ��4xB.y����2x
��4xB.y����2x![]() +4x
+4x
C.y����2x![]() ��4x��4D.y����2x
��4x��4D.y����2x![]() +4x+4
+4x+4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ÿһ��ͼ�о��������ɸ������Σ���1��ͼ����1�������Σ���2��ͼ����1+4��5�������Σ�������ͼ����1+4+9��14�������Σ����������Ĺ�����ȥ����4��ͼ����_____�������Σ�
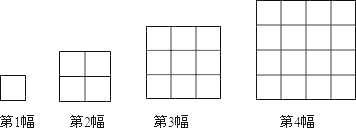
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
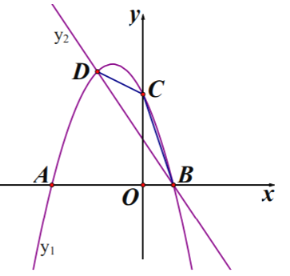
����Ŀ����ͼ�����κ���![]() ��ͼ��
��ͼ��![]() ���㣮
���㣮
��1���۲�ͼ��д��![]() ��������꣬����������߽���ʽ��
��������꣬����������߽���ʽ��
��2���۲�ͼ��![]() ȡ��ֵʱ��
ȡ��ֵʱ��![]() ��
��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com