
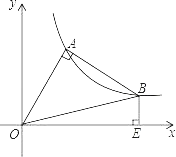
【题目】△OAB在第一象限中,OA=AB,OA⊥AB,O是坐标原点,且函数y=![]() 正好过A,B两点,BE⊥x轴于E点,则OE2﹣BE2的值为( )
正好过A,B两点,BE⊥x轴于E点,则OE2﹣BE2的值为( )
A. 3B. 2C. 3D. 4
【答案】D
【解析】
过点A作AF⊥y轴于点F,延长EB交FA的延长线于点D.由题意可证四边形DEOF是矩形,可得DE=OF,DF=OE,由题意可证△AFO≌△BDA,可得AF=DB, AD=OF,设出A点坐标,表示出BE与OE,即可求出所求式子的值.
如图:过点A作AF⊥y轴于点F,延长EB交FA的延长线于点D.
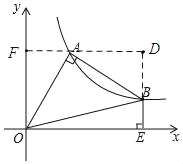
∵AF⊥OF,BE⊥OE,OE⊥OF
∴四边形DEOF是矩形
∴∠D=90°,OF=DE,DF=OE
设点A(a,![]() ),即AF=a,OF=
),即AF=a,OF=![]()
∵∠BAO=90°,AF⊥FO
∴∠BAD+∠FAO=90°,∠FAO+∠FOA=90°
∴∠DAB=∠AOF且AO=AB,∠AFO=∠ADB=90°
∴△AFO≌△BDA(AAS)
∴AD=OF=![]() ,DB=AF=a
,DB=AF=a
∴BE=DE﹣DB=![]() ﹣a,OE=DF=AF+AD=a+
﹣a,OE=DF=AF+AD=a+![]()
∴OE2﹣BE2=(a+![]() )2﹣(
)2﹣(![]() ﹣a)2=4
﹣a)2=4
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=![]() x+6与x、y轴分别交于点A,点B,双曲线的解析式为
x+6与x、y轴分别交于点A,点B,双曲线的解析式为![]()

(1)求出线段AB的长
(2)在双曲线第四象限的分支上存在一点C,使得CB⊥AB,且CB=AB,求k的值;
(3)在(1)(2)的条件下,连接AC,点D为BC的中点,过D作AC的垂线BF,交AC于B,交直线AB于F,连AD,若点P为射线AD上的一动点,连接PC、PF,当点P在射线AD上运动时,PF![]() -PC
-PC![]() 的值是否发生改变?若改变,请求出其范围;若不变,请证明并求出定值。
的值是否发生改变?若改变,请求出其范围;若不变,请证明并求出定值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,抛物线y=ax2+bx+c经过点A(﹣2,0)、B(4,0)、C(0,3)三点.
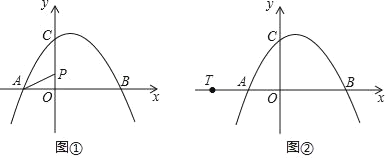
(1)试求抛物线的解析式;
(2)点P是y轴上的一个动点,连接PA,试求5PA+4PC的最小值;
(3)如图②,若直线l经过点T(﹣4,0),Q为直线l上的动点,当以A、B、Q为顶点所作的直角三角形有且仅有三个时,试求直线l的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知梯形ABCD中,AD∥BC,AB=AC,E是边BC上的点,且∠AED=∠CAD,DE交AC于点F.
(1)求证:△ABE∽△DAF;
(2)当ACFC=AEEC时,求证:AD=BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
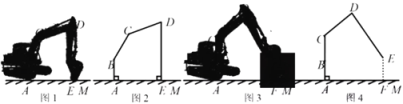
【题目】某挖掘机的底座高AB=0.8米,动臂BC=1.2米,CD=1.5米,BC与CD的固定夹角∠BCD=140°.初始位置如图1,斗杆顶点D与铲斗顶点E所在直线DE垂直地面AM于点E,测得∠CDE=70°(示意图2).工作时如图3,动臂BC会绕点B转动,当点A,B,C在同一直线时,斗杆顶点D升至最高点(示意图4).
(1)求挖掘机在初始位置时动臂BC与AB的夹角∠ABC的度数.
(2)问斗杆顶点D的最高点比初始位置高了多少米(精确到0.1米)?
(考数据:sin50°≈0.77,cos50°≈0.64,sin70°≈0.94,cos70°≈0.34,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,0),B(0,-1),连接AB,过B点作AB的垂线段,使BA=BC,连接AC.
(1)如图1,求C点坐标;
(2)如图2,若P点从A点出发,沿x轴向左平移,连接BP,作等腰直角三角形△BPQ,连接CQ.求证:PA=CQ.
(3)在(2)的条件下,若C、P、Q三点共线,求此时P点坐标及∠APB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘轮船航行到 B 处时,测得小岛 A 在船的北偏东 60°的方向,轮船从 B 处继续向正东方向航行 20 海里到达 C 处时,测得小岛 A 在北船的北偏东 30°的方向.
(1)若小岛 A 到这艘轮船航行路线 BC 的距离是 AD,求 AD 的长.
(2)已知在小岛周围 17 海里内有暗礁,若轮船不改变航向继续向前行驶,试问轮船有无触礁的危险?(![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
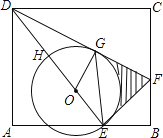
【题目】如图,E是长方形ABCD的边AB上的点,EF⊥DE交BC于点F
(1)求证:△ADE∽△BEF;
(2)设H是ED上一点,以EH为直径作⊙O,DF与⊙O相切于点G,若DH=OH=3,求图中阴影部分的面积(结果保留到小数点后面第一位,![]() ≈1.73,π≈3.14).
≈1.73,π≈3.14).
查看答案和解析>>
科目:初中数学 来源: 题型:
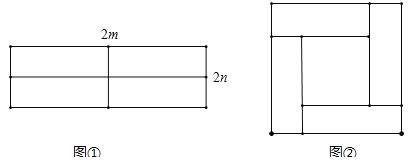
【题目】如图,图①所示是一个长为2m,宽为2n的长方形,用剪刀均分成四个小长方形,然后按图②的方式拼成一个大正方形.
(1)图②中的大正方形的边长等于 ,图②中的小正方形的边长等于 ;
(2)图②中的大正方形的面积等于 ,图②中的小正方形的面积等于 ;图①中每个小长方形的面积是 ;
(3)观察图②,你能写出(m+n)2,(m﹣n)2,mn这三个代数式间的等量关系吗? .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com