Question

如图所示，P₁（x₁，y₁）、P₂（x₂，y₂），…P_n（x_n，y_n）在函数y=

9

x

（x＞0）的图象上，△OP₁A₁，△P₂A₁A₂，△P₃A₂A₃…△P_nA_n-1A_n…都是等腰直角三角形，斜边OA₁，A₁A₂…A_n-1A_n，都在x轴上，
（1）求P₁的坐标．
（2）求A₂的坐标．
（3）直接写出A_n的坐标．

Answer 1

考点：反比例函数综合题

专题：综合题

分析：（1）如图，过点P₁作P₁M⊥x轴，由△OP₁A₁为等腰直角三角形，利用等腰直角三角形的性质得到P₁M=OM=MA₁，设P₁的坐标是（a，a），a＞0，代入反比例解析式求出a的值，即可确定出P₁的坐标；
（2）如图，过点P₂作P₂N⊥x轴，根据OM+A₁M求出OA₁的长，确定出A₁的坐标，再由△P₂A₁A₂为等腰直角三角形，设P₂的纵坐标为b，则P₂横坐标为6+b，代入反比例解析式求出b的长，即可确定出A₂的坐标；
（3）同理确定出A₃，A₄的坐标，归纳总结得到A_n的坐标即可．

解答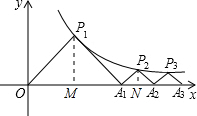：解：（1）如图，过点P₁作P₁M⊥x轴，
∵△OP₁A₁是等腰直角三角形，
∴P₁M=OM=MA₁，
设P₁的坐标是（a，a），a＞0，
把（a，a）代入解析式y=

9

x

（x＞0）中，得a=3，
则P₁的坐标是（3，3）；
（2）如图，过点P₂作P₂N⊥x轴，
∵OM=MA₁=3，
∴OA₁=6，即A₁的坐标是（6，0），
∵△P₂A₁A₂为等腰直角三角形，
∴P₂N=A₁N=A₂N，
设P₂的纵坐标为b，则P₂横坐标为6+b，
把（6+b，b）代入函数解析式得：b=

9

6+b

，
解得：b=6

2

-3，
∴A₂的横坐标为6+2b=6+6

2

-6=6

2

，
则A₂的坐标为（6

2

，0）；
（3）同（2）中的方法得到A₃（6

3

，0），A₄（6

4

，0），
归纳总结得：A_n的横坐标是6

n

．

点评：此题属于反比例函数综合题，涉及的知识有：等腰直角三角形的判定与性质，坐标与图形性质，以及反比例函数的性质，熟练掌握等腰直角三角形的判定与性质是解本题的关键．