
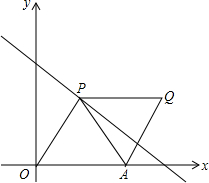
 如图,点P(m,n)是直线y=-x+8上的动点,点A的坐标为(6,0),以PA为对角线,作面积为S的平行四边形OPQA.
如图,点P(m,n)是直线y=-x+8上的动点,点A的坐标为(6,0),以PA为对角线,作面积为S的平行四边形OPQA.分析 (1)点P(m,n)是直线y=-x+8上的动点,所以n=-m+8,然后根据平行四边形的面积=底×高列出函数关系是即可;
(2)当四边形OPQA为矩形时,则∠POA=90°,故此点P在y轴上,令x=0得y=8,从而可求得n=8;
(3)将S=6$\sqrt{2}$+24,代入S与t的关系式,即可求得m的值,然后可求得n,根据勾股定理可求得OP=6,从而可证明四边形为菱形.
解答 解:(1)令y=0得:-x+8=0,解得x=8.
∵点P(m,n)是直线y=-x+8上的动点,
∴n=-m+8.
当m<8时,S=6×(-m+8)=-6m+48;
当m>8时,S=6×(m-8)=6m-48;
∴S与m的函数关系式为S=$\left\{\begin{array}{l}{-6m+48(m<8)}\\{6m-48(m>8)}\end{array}\right.$
(2)当四边形OPQA为矩形时,则∠POA=90°,
∴点P在y轴上.
令x=0得y=8,
∴点P的坐标为(0,8).
∴n=8.
(3)将S=6$\sqrt{2}$+24,代入S=6×(8-m)得:6×(8-m)=6$\sqrt{2}$+24.
解得;m=4-$\sqrt{2}$,则n=4+$\sqrt{2}$,
∴点P的坐标为(4-$\sqrt{2}$,4$+\sqrt{2}$).
∴PO=$\sqrt{{m}^{2}+{n}^{2}}=6$.
∴OP=OA.
又∵四边形OPQA为平行四边形,
∴四边形OPQA为菱形.
点评 本题主要考查的是一次函数与平行四边形、菱形、矩形的综合应用,熟练掌握矩形、菱形的性质是解题的关键.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:选择题
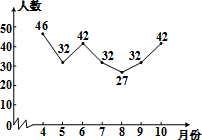 小红根据去年4~10月本班同学去孔学堂听中国传统文化讲座的人数,绘制了如图所示的折线统计图,图中统计数据的众数是( )
小红根据去年4~10月本班同学去孔学堂听中国传统文化讲座的人数,绘制了如图所示的折线统计图,图中统计数据的众数是( )| A. | 46 | B. | 42 | C. | 32 | D. | 27 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
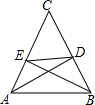 已知锐角△ABC角平分线AD与高线BE交于点M,△CDE是等边三角形,则S△DEM:S△ABM的值为( )
已知锐角△ABC角平分线AD与高线BE交于点M,△CDE是等边三角形,则S△DEM:S△ABM的值为( )| A. | $\sqrt{2}$:2 | B. | 1:2 | C. | 1:3 | D. | 1:4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -8<m≤-6 | B. | -6≤m<-4 | C. | -6<m≤-4 | D. | -8≤m<-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com