
【题目】如图,在矩形纸片ABCD中,AB=6,BC=10,点E在CD上,将△BCE沿BE折叠,点C恰落在边AD上的点F处;点G在AF上,将△ABG沿BG折叠,点A恰落在线段BF上的点H处,有下列结论: ①∠EBG=45°; ②△DEF∽△ABG;
③S△ABG=S△FGH; ④AG+DF=FG.
其中正确的是 . (填写正确结论的序号)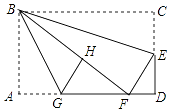
【答案】①④
【解析】解:∵根据折叠得出∠BAG=∠FBG,∠CBE=∠FBE, 又∵四边形ABCD是矩形,
∴∠BAC=90°,
∴∠EBG= ![]() ,∴①正确;
,∴①正确;
∵四边形ABCD是矩形,
∴AB=DC=6,BC=AD=10,∠A=∠C=∠D=90°,
∴根据折叠得∠BFE=∠C=90°,
∴∠ABG+∠BGA=90°,∠EFD+∠BFA=90°,
∵∠BGA>∠BFA,
∴∠BAG≠∠EFD,
∵∠GHB=∠A=90°,∠EFB=∠C=90°,
∴∠GHB=∠EFB,
∴GH∥EF,
∴∠EFD=∠HGF,
根据已知不能推出∠AGB=∠HGF,
∴∠AGB≠∠EFD,
即△DEF和△ABG不全等,∴②错误;
∵根据折叠得:AB=BH=6,BC=BF=10,
∴由勾股定理得:AF= ![]() =8,
=8,
∴DF=10﹣8=2,HF=10﹣6=4,
设AG=HG=x,
在Rt△FGH中,由勾股定理得:GH2+HF2=GF2 ,
即x2+42=(8﹣x)2 ,
解得:x=3,
即AG=HG=3,
∴S△ABG= ![]() =
= ![]() =9,S△FHG=
=9,S△FHG= ![]() =
= ![]() =6,∴③错误;
=6,∴③错误;
∵AG+DF=3+2=5,GF=10﹣3﹣2=5,∴④正确;
故答案为:①④.
根据矩形的性质得出∠A=∠C=∠D=∠ABC=90°,AB=CD=6,BC=AD=10,根据折叠得出∠BAG=∠FBG,∠CBE=∠FBE,AG=GH,BC=BF=10,AB=BH=6,根据勾股定理求出AG=GH=3,再逐个判断即可.


科目:初中数学 来源: 题型:
【题目】对于不等式组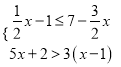 下列说法正确的是( )
下列说法正确的是( )
A. 此不等式组无解 B. 此不等式组有7个整数解
C. 此不等式组的负整数解是﹣3,﹣2,﹣1 D. 此不等式组的解集是![]() <x≤2
<x≤2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
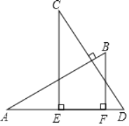
A. a+cB. b+cC. a﹣b+cD. a+b﹣c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
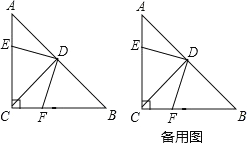
【题目】在△ABC 中,∠ACB=90°,AC=BC,D 是 AB 的中点,点 E 是边 AC 上的一动点,点F 是边 BC 上的一动点.
(1)若 AE=CF,试证明 DE=DF;
(2)在点 E、点 F 的运动过程中,若 DE⊥DF,试判断 DE 与 DF 是否一定相等? 并加以说明.
(3)在(2)的条件下,若 AC=2,四边形 ECFD 的面积是一个定值吗?若不是, 请说明理由,若是,请直接写出它的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点的门票价格规定如表
购票人数 | 1﹣50人 | 51﹣100人 | 100人以上 |
每人门票价 | 12元 | 10元 | 8元 |
某校八年(1)(2)两班共102人去游览该景点,其中(1)班不足50人,(2)班多于50人,如果两班都以班为单位分别购票,则一共付款1118元
(1)两班各有多少名学生?
(2)如果你是学校负责人,你将如何购票?你的购票方法可节省多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绵阳农科所为了考察某种水稻穗长的分布情况,在一块试验田里随机抽取了50个谷穗作为样本,量得它们的长度(单位:cm).对样本数据适当分组后,列出了如下频数分布表:
穗长 | 4.5≤x<5 | 5≤x<5.5 | 5.5≤x<6 | 6≤x<6.5 | 6.5≤x<7 | 7≤x<7.5 |
频数 | 4 | 8 | 12 | 13 | 10 | 3 |
(1)在图1、图2中分别出频数分布直方图和频数折线图;
(2)请你对这块试验田里的水稻穗长进行分析;并计算出这块试验田里穗长在5.5≤x<7范围内的谷穗所占的百分比.
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为2 ![]() 的正方形ABCD中,点E是CD边的中点,延长BC至点F,使CF=CE,连接BE,DF.将△BEC绕点C按顺时针方向旋转.当点E恰好落在DF上的点H处时,连接AG、DG、BG,则AG的长是.
的正方形ABCD中,点E是CD边的中点,延长BC至点F,使CF=CE,连接BE,DF.将△BEC绕点C按顺时针方向旋转.当点E恰好落在DF上的点H处时,连接AG、DG、BG,则AG的长是.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com