
【题目】已知抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴相交于
轴相交于![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),点
左侧),点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,我们称以
,我们称以![]() 为顶点且过点
为顶点且过点![]() ,对称轴与
,对称轴与![]() 轴平行的抛物线为抛物线
轴平行的抛物线为抛物线![]() 的“梦之星”抛物线,直线
的“梦之星”抛物线,直线![]() 为抛物线
为抛物线![]() 的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是
的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是![]() 和
和![]() ,则这条抛物线的解析式为________.
,则这条抛物线的解析式为________.
【答案】![]()
【解析】
先求出y=x2+2x+1和y=2x+2的交点C′的坐标为(1,4),再求出“梦之星”抛物线y=x2+2x+1的顶点A坐标(-1,0),接着利用点C和点C′关于x轴对称得到C(1,-4),则可设顶点式y=a(x-1)2-4,然后把A点坐标代入求出a的值即可得到原抛物线解析式.
∵y=x2+2x+1=(x+1)2,
∴A点坐标为(1,0),
解方程组![]() 得
得![]() 或
或![]() ,
,
∴点C′的坐标为(1,4),
∵点C和点C′关于x轴对称,
∴C(1,4),
设原抛物线解析式为y=a(x1)24,
把A(1,0)代入得4a4=0,解得a=1,
∴原抛物线解析式为y=(x1)24=x22x3.
故答案为y=x22x3.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】如图,BD和CD分别平分△ABC的内角∠EBA和外角∠ECA,BD交AC于F,连接AD.

(1)求证:∠BDC=![]() ∠BAC;
∠BAC;
(2)若AB=AC,请判断△ABD的形状,并证明你的结论;
(3)在(2)的条件下,若AF=BF,求∠EBA的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列文字与例题,并解答。
将一个多项式分组进行因式分解后,可用提公因式法或公式法继续分解的方法称作分组分解法。例如:以下式子的分解因式的方法叉称为分组分解法。
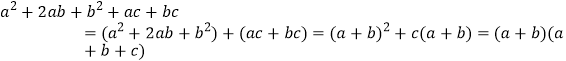 (1)试用“分组分解法”分解因式:
(1)试用“分组分解法”分解因式:![]()
(2)已知四个实数a,b,c,d满足![]() 。并且
。并且![]() ,
,![]() ,
,![]() ,
,![]() 同时成立。
同时成立。
①当k=1时,求a+c的值;
②当k≠0时,用含a的代数式分别表示b、c、d。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某旅行团去景点游览,共有成人和儿童20人,且旅行团中儿童人数多于成人.景点规定:成人票40元/张,儿童票20元/张.
(1)若20人买门票共花费560元,求成人和儿童各多少人?
(2)景区推出“庆元旦”优惠方案,具体方案为:
方案一:购买一张成人票免一张儿童票费用;
方案二:成人票和儿童票都打八折优惠;
设:旅行团中有成人a人,旅行团的门票总费用为W元.
①方案一:![]() _____________________;
_____________________;
方案二:![]() ____________________;
____________________;
②试随着a的变化,哪种方案更优惠?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若所求的二次函数图象与抛物线![]() 有相同的顶点,并且在对称轴的左侧,
有相同的顶点,并且在对称轴的左侧,![]() 随
随![]() 的增大而增大,在对称轴的右侧,
的增大而增大,在对称轴的右侧,![]() 随
随![]() 的增大而减小,则所求二次函数的解析式为( )
的增大而减小,则所求二次函数的解析式为( )
A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设一次函数![]() (k,b是常数,且
(k,b是常数,且![]() ).
).
(1)若该函数的图象过点![]() ,试判断点
,试判断点![]() 是否也在此函数的图象上,并说明理由.
是否也在此函数的图象上,并说明理由.
(2)已知点![]() 和点
和点![]() 都在该一次函数的图象上,求k的值.
都在该一次函数的图象上,求k的值.
(3)若![]() ,点
,点![]()
![]() 在该一次函数图象上,求证:
在该一次函数图象上,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC 中,AB=AC,∠BAC=90,D、E 分别在 BC、AC 边上,连接 AD、BE 相交于点 F,且∠CAD=![]() ∠ABE.
∠ABE.

(1)求证:BF=AC;
(2)如图2,连接 CF,若 EF=EC,求∠CFD 的度数;
(3)如图3,在⑵的条件下,若 AE=3,求 BF 的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com