
【题目】如图,在平面直角坐标系中,正方形![]() 的边长为
的边长为![]() ,顶点
,顶点![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴,抛物线
轴的正半轴,抛物线![]() 经过
经过![]() 两点,点
两点,点![]() 为抛物线的顶点,连接
为抛物线的顶点,连接![]() .
.
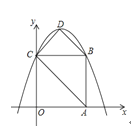
(1)求此抛物线的解析式;
(2)直接写出四边形![]() 的面积.
的面积.
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(m-1)x2-x-2=0,
(1)若x=-1是方程的一个根,求m的值及另一个根;
(2)当m为何值时方程有两个不同的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年非洲猪瘟疫情暴发后,今年猪肉价格不断走高,引起了民众与政府的高度关注,据统计:今年7月20日猪肉价格比今年年初上涨了60%,某市民今年7月20日在某超市购买1千克猪肉花了80元钱.
(1)问:今年年初猪肉的价格为每千克多少元?
(2)某超市将进货价为每千克65元的猪肉,按7月20日价格出售,平均一天能销售出100千克,经调查表明:猪肉的售价每千克下降1元,其日销售量就增加10千克,超市为了实现销售猪内每天有1560元的利润,并且可能让顾客得到实惠,猪肉的售价应该下降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据农业农村部新闻部办公室2018年10月15日消息,江宁省发现疑似非洲猪瘟疫情,此次猪瘟疫情发病急,蔓延速度快.当政府和企业迅速进行了猪瘟疫情排查和处置,在疫情排查过程中,某农场第一天发现3头生猪发病,两天后发现共有192头生猪发病,
(1)求每头发病生猪平均每天传染多少头生猪?
(2)若疫情得不到有效控制,3天后生猪发病头数会超过1500头吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,![]() 中,
中,![]() ,动点
,动点![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动,过点
运动,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的平行线,与过点
的平行线,与过点![]() 且与
且与![]() 垂直的直线交于点
垂直的直线交于点![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() (秒)
(秒)![]()
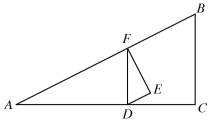
(1)用含![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
(2)求当点![]() 落在
落在![]() 边上时t的值;
边上时t的值;
(3)设![]() 与
与![]() 重合部分图形的面积为
重合部分图形的面积为![]() (平方单位),求
(平方单位),求![]() 与的
与的![]() 函数关系式;
函数关系式;
(4)连结![]() ,若将
,若将![]() 沿它自身的某边翻折,翻折前后的两个三角形形成菱形,直接写出此时
沿它自身的某边翻折,翻折前后的两个三角形形成菱形,直接写出此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】城市中“打车难”一直是人们关注的一个社会热点问题.近几年来,“互联网+”战略与传统出租车行业深度融合,“优步”、“滴滴出行”等打车软件就是其中典型的应用,名为“数据包络分析”(简称DEA)的一种效率评价方法,可以很好地优化出租车资源配置,为了解出租车资源的“供需匹配”,北京、上海等城市对每天24个时段的DEA值进行调查,调查发现,DEA值越大,说明匹配度越好.在某一段时间内,北京的DEA值y与时刻t的关系近似满足函数关系![]() (a,b,c是常数,且
(a,b,c是常数,且![]() ≠0),如图记录了3个时刻的数据,根据函数模型和所给数据,当“供需匹配”程度最好时,最接近的时刻t是( )
≠0),如图记录了3个时刻的数据,根据函数模型和所给数据,当“供需匹配”程度最好时,最接近的时刻t是( )

A. 4.8 B. 5 C. 5.2 D. 5.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)某学校“智慧方园”数学社团遇到这样一个题目:
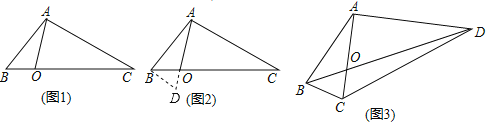
如图1,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=![]() ,BO:CO=1:3,求AB的长.
,BO:CO=1:3,求AB的长.
经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2).
请回答:∠ADB= °,AB= .
(2)请参考以上解决思路,解决问题:
如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=![]() ,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象过点
的图象过点![]() 、顶点
、顶点![]() 的横坐标为.
的横坐标为.
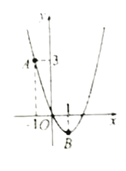
(1)求这个二次函数的解析式;
(2)点![]() 在该一次函数的图象上,点
在该一次函数的图象上,点![]() 在
在![]() 轴上,若以
轴上,若以![]() 为顶点的四边形是平行四边形,求点
为顶点的四边形是平行四边形,求点![]() 的坐标。
的坐标。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com