
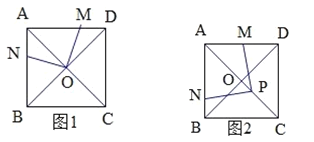
【题目】已知正方形ABCD的对角线相交于O,点P在射线AO上,∠MPN=90°.
(1)如图1,当P与点O重合,M、N分别在AD、AB上,AM=2DM,则![]() =__________;
=__________;
(2)如图2,点P在CO上,AP=2CP,M为AD的中点,求![]() 的值.
的值.
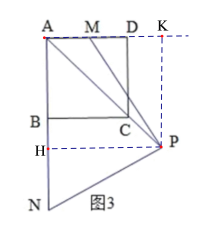
(3)如图3,P在AC的延长线上,M为AD的中点,AP=nCP,则![]() =____________(用含n的式子表示)
=____________(用含n的式子表示)

【答案】(1)![]() ;(2)
;(2)![]() =5;(3)
=5;(3)![]()
【解析】
(1)根据正方形的性质定理和三角形全等的判定定理,可得MODNOA,MOANOB,结合AM=2DM,即可得到结论;
(2)过点P作PF∥AD,PE∥AB,易得AE=2ED,设ED=a,则AE=2a,A =3a,MD=![]() ,ME =
,ME =![]() a,再证MEPNFP,可得AN=
a,再证MEPNFP,可得AN=![]() ,BN=
,BN=![]() a,进而即可得到结论;
a,进而即可得到结论;
(3)过点P作PK⊥AD交AD的延长线于点K,过点P作PH⊥AN于点H,易得![]() ,设DK=a,则AK=na,AD=(n-1)a,MK=
,设DK=a,则AK=na,AD=(n-1)a,MK=![]() ,由(2)题的方法得:MKPNHP,从而得AN=
,由(2)题的方法得:MKPNHP,从而得AN=![]() ,BN=
,BN=![]() ,进而即可得到结论.
,进而即可得到结论.
(1)∵正方形ABCD的对角线相交于O,
∴OA=OD,∠ODM=∠OAN=45°,∠AOD=90°,
∵∠MPN=90°,
∴∠MOD+∠AOM=∠NOA+∠AOM=90°,
∴∠MOD=∠NOA,
∴MODNOA(ASA),
∴DM=NA,
同理:MOANOB(ASA),
∴AM=BN,
∵AM=2DM,
∴BN=2 NA
∴![]() =
=![]() ,
,
故答案是:![]() ;
;
(2)过点P作PF∥AD,PE∥AB,
∴![]() ,
,
∵AP=2CP,
∴AE=2ED,
设ED=a,则AE=2a,AD=2a+a=3a,
∵M为AD的中点,
∴MD=![]() AD=
AD=![]() ×3a=
×3a=![]() ,ME=
,ME=![]() - a=
- a=![]() a,
a,
∵FG∥AD,PE∥AB,
∴PF⊥AB,PE⊥AD,
∵AC是∠BAD的平分线,
∴PF=PE,
∵∠BAD=90°,
∴四边形AEPF是正方形,即:∠EPF=90°,
∵∠MPN=90°,
∴∠EPM+∠MPF=∠FPN+∠MPF=90°,
∴∠EPM=∠FPN,
又∵∠MEP=∠NFP=90°,
∴MEPNFP(ASA),
∴ME=NF=![]() a,
a,
又∵AF=AE=2a,
∴AN=2a+![]() a=
a=![]() ,
,
∵AB=AD=3a,
∴BN=3a-![]() =
=![]() a,
a,
∴![]() =5;
=5;
(3)过点P作PK⊥AD交AD的延长线于点K,过点P作PH⊥AN于点H,
∵PK∥CD,AP=nCP,
∴![]() ,
,
设DK=a,则AK=na,AD=(n-1)a,
∵M为AD的中点,
∴MD=![]() ,
,
∴MK=MD+DK=![]() ,
,
由(2)题的方法得:MKPNHP(AAS),四边形AKPH是正方形,
∴HN=MK=![]() ,AH=AK=na,
,AH=AK=na,
∴AN=![]() +na=
+na=![]() ,BN=
,BN=![]() -(n-1)a=
-(n-1)a=![]() ,
,
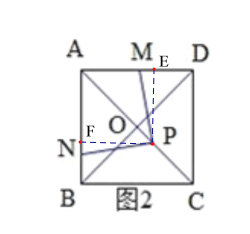
∴![]() =
=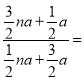
![]() .
.
故答案是:![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2)延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x 轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2018个正方形的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(b≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标(﹣1,0),下面的四个结论:①OA=3 ②a+b+c<0 ③ac>0 ④当y>0时,﹣1<x<3,其中正确的结论是( )
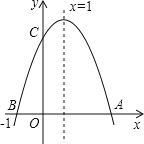
A.②④B.①③C.①④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与坐标轴分别交于A,B,C,点D在x轴上,AC=CD,过点D作DE⊥x轴交抛物线于点E,点P,Q分别是线段CO,CD上的动点,且CP=QD.记△APC的面积为S1,△PCQ的面积为S2,△QED的面积为S3,
与坐标轴分别交于A,B,C,点D在x轴上,AC=CD,过点D作DE⊥x轴交抛物线于点E,点P,Q分别是线段CO,CD上的动点,且CP=QD.记△APC的面积为S1,△PCQ的面积为S2,△QED的面积为S3,
(1)若S1+S3=4S2 ,求Q点坐标;
(2)连结AQ,求AP+AQ的最小值;
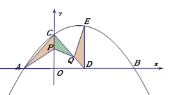
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (
(![]() ,
,![]() 为常数,
为常数,![]() )的图象记为L.
)的图象记为L.
(1)若![]() =1,
=1,![]() =3,求图象L的顶点坐标;
=3,求图象L的顶点坐标;
(2)若图象L过点(4,1),且2≤a≤5,求![]() 的最大值;
的最大值;
(3)若![]() ,点
,点![]() ,
,![]() 在图象L上,当
在图象L上,当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京第一条地铁线路于1971年1月15日正式开通运营.截至2017年1月,北京地铁共“金山银山,不如绿水青山”.某市不断推进“森林城市”建设,今春种植四类树苗,园林部门从种植的这批树苗中随机抽取了4000棵,将各类树苗的种植棵数绘制成扇形统计图,将各类树苗的成活棵数绘制成条形统计图,经统计松树和杨树的成活率较高,且杨树的成活率为97%,根据图表中的信息解答下列问题:
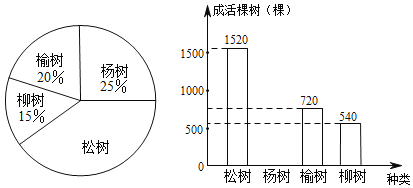
(1)扇形统计图中松树所对的圆心角为 度,并补全条形统计图.
(2)该市今年共种树16万棵,成活了约多少棵?
(3)园林部门决定明年从这四类树苗中选两类种植,请用列表法或树状图求恰好选到成活率较高的两类树苗的概率.(松树、杨树、榆树、柳树分别用A,B,C,D表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
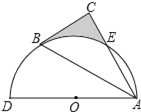
【题目】如图,以AD为直径的半圆O经过Rt△ABC斜边AB的两个端点,交直角边AC于点E,B、E是半圆弧的三等分点,弧BE的长为![]() π,则图中阴影部分的面积为( )
π,则图中阴影部分的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() (a,b,c为常数,且
(a,b,c为常数,且![]() )经过点(﹣1,0)和(m,0),且1<m<2,当x<﹣1时,y随着x的增大而减小.下列结论:
)经过点(﹣1,0)和(m,0),且1<m<2,当x<﹣1时,y随着x的增大而减小.下列结论:
①abc>0;
②a+b>0;
③若点A(﹣3,![]() ),点B(3,
),点B(3,![]() )都在抛物线上,则
)都在抛物线上,则![]() <
<![]() ;
;
④![]() ;
;
⑤若若![]() ,则
,则![]() .
.
其中结论错误的是 .(只填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)中的x和y满足下表:
x | … | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 3 | 0 | -1 | 0 | m | 8 | … |
(1)可求得m的值为________;
(2)在坐标系画出该函数的图象;
(3)当y≥0时,x的取值范围为_____________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com