
【题目】(操作发现)
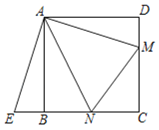
如图①,在正方形ABCD中,点N、M分别在边BC、CD上,连结AM、AN、MN.
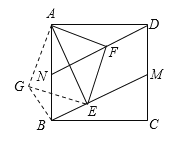
∠MAN=45°,将△AMD绕点A顺时针旋转90°,点D与点B重合,得到△ABE.易证:△ANM≌△ANE,从而得DM+BN=MN.
(实践探究)
(1)在图①条件下,若CN=3,CM=4,则正方形ABCD的边长是 .
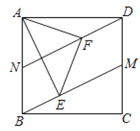
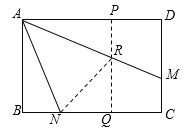
(2)如图②,点M、N分别在边CD、AB上,且BN=DM.点E、F分别在BM、DN上,∠EAF=45°,连接EF,猜想三条线段EF、BE、DF之间满足的数量关系,并说明理由.
(拓展)
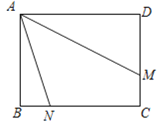
(3)如图③,在矩形ABCD中,AB=3,AD=4,点M、N分别在边DC、BC上,连结AM,AN,已知∠MAN=45°,BN=1,求DM的长.
【答案】(1)6;(2)![]() ,见解析;(3)2
,见解析;(3)2
【解析】
(1)根据旋转的性质证明△ABE≌△ADM得到BE=DM,又由∠ABE=∠D=90°,AE=AM,∠BAE=∠DAM,证出∠EAM=90°,得出∠MAN=∠EAN,再证明△AMN≌△EAN(SAS),得出MN=EN最后证出MN=BN+DM.在Rt△CMN中,由勾股定理计算即可得到正方形的边长;
(2 )先根据旋转的性质证明△AEG≌△AEF(SAS),再证明∠GBE=90°,再根据勾股定理即可得到;
(3)在AB上截取AP,在BC上截取BQ,使AP=AB=BQ=3,连结PQ交AM于点R,得到ABQP为正方形,再根据操作发现以及勾股定理即可得到答案;
(1)(1)解:∵四边形ABCD是正方形,
∴AB=CD=AD,∠BAD=∠C=∠D=90°,
由旋转得:△ABE≌△ADM,
∴BE=DM,∠ABE=∠D=90°,AE=AM,∠BAE=∠DAM,
∴∠BAE+∠BAM=∠DAM+∠BAM=∠BAD=90°,
即∠EAM=90°,
∵∠MAN=45°,
∴∠EAN=90°-45°=45°,
∴∠MAN=∠EAN,
在△AMN和△EAN中,
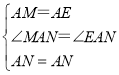
∴△AMN≌△EAN(SAS),
∴MN=EN.
∵EN=BE+BN=DM+BN,
∴MN=BN+DM.
在Rt△CMN中,
![]() ,
,
则BN+DM=5,
设正方形ABCD的边长为x,则BN=BC-CN=x-3,DM=CD-CM=x-4,
∴x-3+x-4=5,
解得:x=6,
即正方形ABCD的边长是6;
故答案为:6;
(2)数量关系为:![]() ,证明如下:
,证明如下:
将△AFD绕点A顺时针旋转90°,点D与点B重合,得到△ABG,连结EG.
由旋转的性质得到:AF=AG,![]()
又∵∠EAF=45°,
∴![]() ,
,
且AE=AE,
∴△AEG≌△AEF(SAS),
从而得EG=EF.(全等三角形对应边相等),
又∵BN=DM,BN∥DM,
∴四边形DMBN是平行四边形(一组对边平行且相等的四边形是平行四边形),
∴DN∥BM,
∴![]() (两直线平行,同位角相等),
(两直线平行,同位角相等),
∵![]() ,
,
∴![]() (等量替换),
(等量替换),
即:∠GBE=90°,
则![]() ,
,
∴![]() ;
;
(3)在AB上截取AP,在BC上截取BQ,使AP=AB=BQ=3,连结PQ交AM于点R,
易证ABQP为正方形,
由操作与发现知:PR+BN=RN.
设PR=x,则RQ=3﹣x,RN=1+x,QN=3-1=2
在Rt△QRN中,由勾股定理得:
![]() ,
,
即![]()
解得:x=![]() ,
,
∴PR=![]()
∵PQ∥DC,
∴△APR∽△ADM,
∴![]() (相似三角形对应边成比例)
(相似三角形对应边成比例)
∴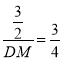
∴DM=2;


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】如图,已知AB为半圆O的直径,C为半圆O上一点,连接AC,BC,过点O作OD⊥AC于点D,过点A作半圆O的切线交OD的延长线于点E,连接BD并延长交AE于点F.
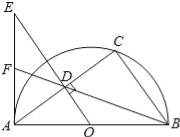
(1)求证:AEBC=ADAB;
(2)若半圆O的直径为10,sin∠BAC=![]() ,求AF的长.
,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:
已知![]() 是正方形
是正方形![]() 的对角线,将正方形
的对角线,将正方形![]() 和正方形
和正方形![]() 按如图放置.
按如图放置.
(1)如图1,使点![]() 与点
与点![]() 重合,
重合,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() .求证:
.求证:![]() .
.
操作发现:
图1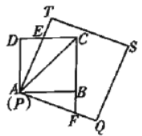
(2)如图2,使点![]() 在
在![]() 上(
上(![]() ,
,![]() 两点除外),
两点除外),![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 的延长线相交于点
的延长线相交于点![]() .判断
.判断![]() 和
和![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
图2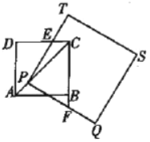
拓广探索:
(3)如图3,使![]() 在
在![]() 上(
上(![]() ,
,![]() 两点除外),
两点除外),![]() 经过点
经过点![]() ,
,![]() 与正方形
与正方形![]() 的外角
的外角![]() 的平分线
的平分线![]() 相交于点
相交于点![]() .判断
.判断![]() 和
和![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
图3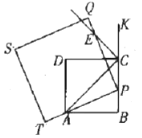
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OEOP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE=![]() ,其中正确的结论是( )
,其中正确的结论是( )
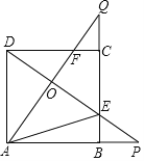
A.①③B.①②③C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2020盐城国际半程马拉松”的赛事共有三项:A、“半程马拉松”、B、“10公里”、C、“迷你马拉松”.小明和小华参加了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组.
(1)小明被分配到“迷你马拉松”项目组的概率为 ;
(2)请用表格或树状图列出所有可能情况,求小明和小华被分配到不同项目组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)作图:作∠MON的平分线OE,在OE上任取一点A,过A作AB∥OM,AC∥ON,连接BC交OA于D.(只保留作图痕迹)

(2)BC与OA的位置关系是什么?请加以证明.
(3)若OA=8,AC=5,则BD是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年9月,我国中小学生迎来了新版“教育部统编义务教育语文教科书”,本次“统编本”教材最引人关注的变化之一是强调对传统文化经典著作的阅读,某校对A《三国演义》、B《红楼梦》、C《西游记》、D《水浒》四大名著开展“最受欢迎的传统文化经典著作”调查,随机调查了若干名学生(每名学生必选且只能选这四大名著中的一部)并将得到的信息绘制了下面两幅不完整的统计图:

(1)本次一共调查了 名学生;
(2)请将条形统计图补充完整;
(3)某班语文老师想从这四大名著中随机选取两部作为学生暑期必读书籍,请用树状图或列表的方法求恰好选中《三国演义》和《红楼梦》的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一项工程,甲队单独做需40天完成,若乙队先做30天后,甲、乙两队一起合做20天恰好完成任务,请问:
(1)乙队单独做需要多少天才能完成任务?
(2)现将该工程分成两部分,甲队做其中一部分工程用了x天,乙队做另一部分工程用了y天,若x; y都是正整数,且甲队做的时间不到15天,乙队做的时间不到70天,那么两队实际各做了多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一家蔬菜公司收购到某种绿色蔬菜140吨,准备加工后进行销售,销售后获利的情况如下表所示:
销售方式 | 粗加工后销售 | 精加工后销售 |
每吨获利(元) | 1000 | 2000 |
已知该公司的加工能力是:每天能精加工5吨或粗加工15吨,但两种加工不能同时进行.受季节等条件的限制,公司必须在一定时间内将这批蔬菜全部加工后销售完.
(1)如果要求12天刚好加工完140吨蔬菜,则公司应安排几天精加工,几天粗加工?
(2)如果先进行精加工,然后进行粗加工.
①试求出销售利润![]() 元与精加工的蔬菜吨数
元与精加工的蔬菜吨数![]() 之间的函数关系式;
之间的函数关系式;
②若要求在不超过10天的时间内,将140吨蔬菜全部加工完后进行销售,则加工这批蔬菜最多获得多少利润?此时如何分配加工时间?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com