练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】“2020盐城国际半程马拉松”的赛事共有三项：A、“半程马拉松”、B、“10公里”、C、“迷你马拉松”．小明和小华参加了该项赛事的志愿者服务工作，组委会随机将志愿者分配到三个项目组．

    （1）小明被分配到“迷你马拉松”项目组的概率为　 　；

    （2）请用表格或树状图列出所有可能情况，求小明和小华被分配到不同项目组的概率．

    【答案】（1）；（2）

    【解析】

    （1）直接利用概率公式求解；

    （2）画树状图展示所有9种等可能的结果数，找出小明和小华被分配到不同项目组的结果数，然后根据概率公式求解．

    解：（1）小明被分配到“迷你马拉松”项目组的概率为；

    故答案为；

    （2）画树状图为：

    共有9种等可能的结果数，其中小明和小华被分配到不同项目组的结果(A,B)(A,C)(B,A)(B,C)(C,A)(C,B)数为6，

    所以小明和小华被分配到不同项目组的概率P＝＝．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

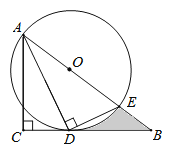
    【题目】如图，在△ABC中，∠C=90°，∠BAC的平分线AD交BC于点D，过点D作DE⊥AD交AB于点E，以AE为直径作⊙O．

    （1）求证：直线BC是⊙O的切线；

    （2）若∠ABC=30°，⊙O的直径为4，求阴影部分面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

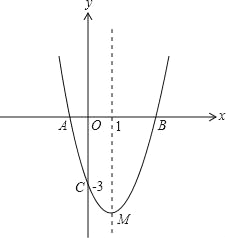
    【题目】（11分）如图，抛物线y=ax2+bx﹣3与x轴交于A，B两点，与y轴交于C点，且经过点（2，﹣3a），对称轴是直线x=1，顶点是M．

    （1）求抛物线对应的函数表达式；

    （2）经过C，M两点作直线与x轴交于点N，在抛物线上是否存在这样的点P，使以点P，A，C，N为顶点的四边形为平行四边形？若存在，请求出点P的坐标；若不存在，请说明理由；

    （3）设直线y=﹣x+3与y轴的交点是D，在线段BD上任取一点E（不与B，D重合），经过A，B，E三点的圆交直线BC于点F，试判断△AEF的形状，并说明理由；

    （4）当E是直线y=﹣x+3上任意一点时，（3）中的结论是否成立（请直接写出结论）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

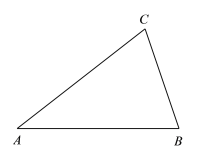
    【题目】如图，已知△ABC中，AB＝AC．

    （1）把△ABC绕点C顺时针旋转得到△DEC，使得点B的对应点E落在AB边上，用尺规作图的方法作出△DEC；（保留作图痕迹，不写作法）

    （2）在（1）的条件下，连接AD，求证：AD＝BC．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等腰Rt△ABP的斜边AB=2，点M、N在斜边AB上．若△PMN是等腰三角形且底角正切值为2，则MN＝_________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（操作发现）

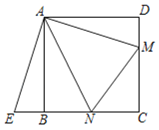
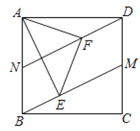
    如图①，在正方形ABCD中，点N、M分别在边BC、CD上，连结AM、AN、MN．

    ∠MAN＝45°，将△AMD绕点A顺时针旋转90°，点D与点B重合，得到△ABE．易证：△ANM≌△ANE，从而得DM+BN＝MN．

    （实践探究）

    （1）在图①条件下，若CN＝3，CM＝4，则正方形ABCD的边长是 　．

    （2）如图②，点M、N分别在边CD、AB上，且BN＝DM．点E、F分别在BM、DN上，∠EAF＝45°，连接EF，猜想三条线段EF、BE、DF之间满足的数量关系，并说明理由．

    （拓展）

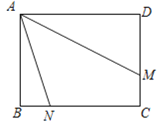
    （3）如图③，在矩形ABCD中，AB＝3，AD＝4，点M、N分别在边DC、BC上，连结AM，AN，已知∠MAN＝45°，BN＝1，求DM的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】南宁市金陵镇三联村无公害蔬菜基地有甲、乙两种植户，他们种植了A、B两类蔬菜，两种植户种植的两类蔬菜的种植面积与总收入如下表：

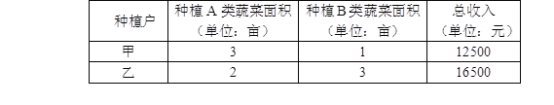
    说明：不同种植户种植的同类蔬菜每亩平均收入相等．

    （1）求A、B两类蔬菜每亩平均收入各是多少元？

    （2）某种植户准备租20亩地用来种植A、B两类蔬菜，为了使总收入不低于63000元，且种植A类蔬菜的面积多于种植B类蔬菜的面积（两类蔬菜的种植面积均为整数），求该种植户所有租种方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

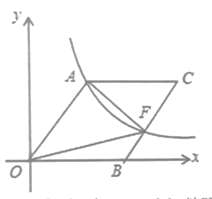
    【题目】如图，在直角坐标系中，四边形OACB为菱形，OB在x轴的正半轴上，∠AOB=60°，过点A的反比例函数y= 的图像与BC交于点F，则△AOF的面积为 ______________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等边△ABC的顶点A(1，1)，B(3，1)，规定把△ABC“先沿x轴翻折，再向左平移1个单位”为一次变换，这样连续经过2020次变换后，等边△ABC的顶点C的坐标为（ ）

    A.(－2 020，)B.(－2 019，)

    C.(－2 018，)D.(－2 017，)

    查看答案和解析>>

    同步练习册答案