
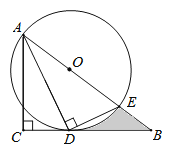
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线AD交BC于点D,过点D作DE⊥AD交AB于点E,以AE为直径作⊙O.
(1)求证:直线BC是⊙O的切线;
(2)若∠ABC=30°,⊙O的直径为4,求阴影部分面积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接OD,由AE为直径、DE⊥AD可得出点D在⊙O上且∠DAO=∠ADO,根据AD平分∠CAB可得出∠CAD=∠DAO=∠ADO,由“内错角相等,两直线平行”可得出AC∥DO,再结合∠C=90°即可得出∠ODB=90°,进而即可证出BC是⊙O的切线;
(2)由题意得出AE=4,DO=AO=EO=![]() AE=2,由直角三角形的性质得出CD,DE,由勾股定理求出AD,AC,由三角函数求出BC,由三角形面积、梯形面积和扇形面积公式即可得出答案.
AE=2,由直角三角形的性质得出CD,DE,由勾股定理求出AD,AC,由三角函数求出BC,由三角形面积、梯形面积和扇形面积公式即可得出答案.
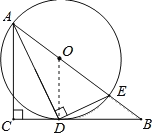
(1)连接OD,如图所示.
在Rt△ADE中,点O为AE的中心,
∴DO=AO=EO=![]() AE,
AE,
∴点D在⊙O上,且∠DAO=∠ADO.
∵AD平分∠CAB,
∴∠CAD=∠DAO,
∴∠ADO=∠CAD,
∴AC∥DO.
∵∠C=90°,
∴∠ODB=90°,即OD⊥BC.
∵OD为半径,
∴BC是⊙O的切线;
(2)∵⊙O的直径为4,
∴AE=4,DO=AO=EO=![]() AE=2.
AE=2.
∵∠ABC=30°,
∴∠CAD=∠DAO=30°,
∴CD=![]() AD,DE=
AD,DE=![]() AE=2,AD=
AE=2,AD=![]() =2
=2![]() ,
,
∴CD=![]() ,AC=
,AC=![]() =3.
=3.
∵tan∠ABC=![]() ,
,
∴BC=3![]() ,
,
∴阴影部分面积=S△ABC﹣S梯形ODCA﹣S扇形ODE
=![]() ACBC﹣
ACBC﹣![]() (OD+AC)CD﹣
(OD+AC)CD﹣![]()
=![]() ×3×3
×3×3![]() ﹣
﹣![]() (2+3)×
(2+3)×![]() ﹣
﹣![]()
=2![]() ﹣
﹣![]() π.
π.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,O为AC、BD的交点,△DCE为Rt△,∠CED=90°,OE=![]() ,若CE
,若CE![]() DE=5,则正方形的面积为( )
DE=5,则正方形的面积为( )
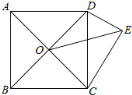
A.5B.6C.7D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
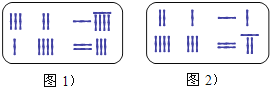
【题目】《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是![]() ,类似地,图2所示的算筹图我们可以表述为( )
,类似地,图2所示的算筹图我们可以表述为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某赛季甲、乙两名篮球运动员12场比赛得分情况用图表示如下:
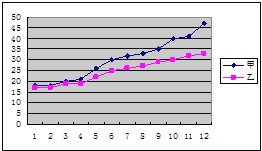
对这两名运动员的成绩进行比较,下列四个结论中,不正确的是( )
A.甲运动员得分的极差大于乙运动员得分的极差B.甲运动员得分的的中位数大于乙运动员得分的的中位数
C.甲运动员的得分平均数大于乙运动员的得分平均数D.甲运动员的成绩比乙运动员的成绩稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学了尺规作图后,通过“三弧法”作了一个△ACD,其作法步骤是:①作线段AB,分别以A,B为圆心,AB长为半径画弧,两弧的交点为C;②以B为圆心,AB长为半径画弧交AB的延长线于点D;③连结AC,BC,CD.下列说法不正确的是( )

A.∠A=60°B.△ACD是直角三角形
C.BC=![]() CDD.点B是△ACD的外心
CDD.点B是△ACD的外心
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB为半圆O的直径,C为半圆O上一点,连接AC,BC,过点O作OD⊥AC于点D,过点A作半圆O的切线交OD的延长线于点E,连接BD并延长交AE于点F.
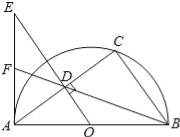
(1)求证:AEBC=ADAB;
(2)若半圆O的直径为10,sin∠BAC=![]() ,求AF的长.
,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人准备整理一批新到的实验器材,若甲单独整理需要40分钟完工,若甲、乙共同整理20分钟后,乙需再单独整理20分钟才能完工.
⑴问乙单独整理多少分钟完工?
⑵若乙因工作需要,他的整理时间不超过30分钟,则甲至少整理多少分钟才能完工?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为改善办学条件,计划购进A,B两种规格的书架,经市场调查发现有线下和线上两种购买方式,具体情况如下表:

(1)如果在线下购买A,B两种书架20个,共花费5520元,求A,B两种书架各购买了多少个.
(2)如果在线上购买A,B两种书架20个,共花费W元,设其中A种书架购买m个,求W关于m的函数关系式.
(3)在(2)的条件下,若购买B种书架的数量不少于A种书架数量的2倍,请求出花费最少的购买方案,并计算按照这种购买方案,线上比线下节约多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2020盐城国际半程马拉松”的赛事共有三项:A、“半程马拉松”、B、“10公里”、C、“迷你马拉松”.小明和小华参加了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组.
(1)小明被分配到“迷你马拉松”项目组的概率为 ;
(2)请用表格或树状图列出所有可能情况,求小明和小华被分配到不同项目组的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com