
【题目】随着地铁和共享单车的发展,“地铁![]() 单车”已成为很多市民出行的选择,李华从学院路站出发,先乘坐地铁,准备在离家较近的
单车”已成为很多市民出行的选择,李华从学院路站出发,先乘坐地铁,准备在离家较近的![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 中的某一站出地铁,再骑共享单车回家,设他出地铁的站点与学院路距离为
中的某一站出地铁,再骑共享单车回家,设他出地铁的站点与学院路距离为![]() (单位:千米),乘坐地铁的时间
(单位:千米),乘坐地铁的时间![]() (单位:分钟)是关于
(单位:分钟)是关于![]() 的一次函数,其关系如下表:
的一次函数,其关系如下表:
地铁站 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(![]() )求
)求![]() 关于
关于![]() 的函数表达式.
的函数表达式.
(![]() )李华骑单车的时间
)李华骑单车的时间![]() (单位:分钟)与
(单位:分钟)与![]() 的关系式为
的关系式为![]() ,求李华从学院路站回到家的最短总时间,并指出他在哪一站出地铁.
,求李华从学院路站回到家的最短总时间,并指出他在哪一站出地铁.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】2016年9月,某手机公司发布了新款智能手机,为了调查某小区业主对该款手机的购买意向,该公司在某小区随机对部分业主进行了问卷调查,规定每人只能从A类(立刻去抢购)、B类(降价后再去买)、C类(犹豫中)、D类(肯定不买)这四类中选一类,并制成了以下两幅不完整的统计图,由图中所给出的信息解答下列问题:
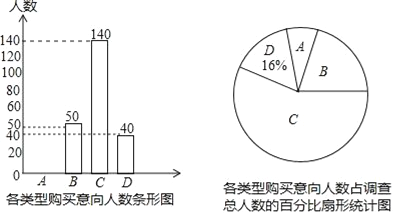
(1)扇形统计图中B类对应的百分比为 %,请补全条形统计图;
(2)若该小区共有4000人,请你估计该小区大约有多少人立刻去抢购该款手机.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明解方程![]() 出现了错误,解答过程如下:
出现了错误,解答过程如下:
方程两边都乘以![]() ,得
,得![]() . (第一步)
. (第一步)
去括号,得 ![]() . (第二步)
. (第二步)
移项,合并同类项,得 ![]() . (第三步)
. (第三步)
解得 ![]() . (第四步)
. (第四步)
经检验,![]() 是原方程的解. (第五步)
是原方程的解. (第五步)
(1)小明解答过程是从第 步开始出错的,原方程化为第一步的根据是 .
(2)请写出此题正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
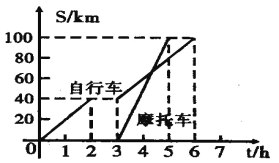
【题目】已知有两人分别骑自行车和摩托车沿着相同的路线从甲地到乙地去,下图反映的是这两个人行驶过程中路程s(km)和时间t(h)的关系,请根据图象回答下列问题:
(1)甲地与乙地相距 千米.
(2)摩托车比自行车晚出发 小时.
(3)求摩托车行驶的路程s与时间t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知: ![]() 在直角坐标平面内,三个顶点的坐标分别为
在直角坐标平面内,三个顶点的坐标分别为![]() ,
, ![]() ,
, ![]() (正方形网格中每个小正方形边长是
(正方形网格中每个小正方形边长是![]() 个单位长度)
个单位长度)
(![]() )
)![]() 是
是![]() 绕点__________逆时针旋转__________度得到的,
绕点__________逆时针旋转__________度得到的, ![]() 的坐标是__________.
的坐标是__________.
(![]() )求出线段
)求出线段![]() 旋转过程中所扫过的面积(结果保留
旋转过程中所扫过的面积(结果保留![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴,M为它的顶点
(1)求抛物线的函数关系式;
(2)求△MCB的面积;
(3)设点P是直线l上的一个动点,当PA+PC最小时,求最小值。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人先后从公园大门出发,沿绿道向码头步行,乙先到码头并在原地等甲到达.图1是他们行走的路程y(m)与甲出发的时间x(min)之间的函数图象.
(1)求线段AC对应的函数表达式;
(2)写出点B的坐标和它的实际意义;
(3)设d(m)表示甲、乙之间的距离,在图2中画出d与x之间的函数图象(标注必要数据).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲学校到乙学校有A1、A2、A3三条线路,从乙学校到丙学校有B1、B2二条线路.
(1)利用树状图或列表的方法表示从甲学校到丙学校的线路中所有可能出现的结果;
(2)小张任意走了一条从甲学校到丙学校的线路,求小张恰好经过了B1线路的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠1=∠2,DB=DC.
(1)求证:△ABD≌△EDC;
(2)若∠A=135°,∠BDC=30°,求∠BCE的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com