练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

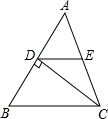
    如图，△ABC中，CD⊥AB于D，E是AC的中点．若AD=6，DE=5，则CD的长等于__________．


    8．

    【考点】勾股定理；直角三角形斜边上的中线．

    【专题】计算题．

    【分析】由“直角三角形斜边上的中线等于斜边的一半”求得AC=2DE=10；然后在直角△ACD中，利用勾股定理来求线段CD的长度即可．

    【解答】解：如图，∵△ABC中，CD⊥AB于D，E是AC的中点，DE=5，

    ∴DE=AC=5，

    ∴AC=10．

    在直角△ACD中，∠ADC=90°，AD=6，AC=10，则根据勾股定理，得

    CD===8．

    故答案是：8．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，把Rt△ABC（∠C=90°）折叠，使A、B两点重合，得到折痕ED，再沿BE折叠，C点恰好与D点重合，则∠A等于__________度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


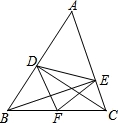
    如图，在△ABC中，CD⊥AB于点D，BE⊥AC于点E，F为BC的中点，DE=5，BC=8，则△DEF的周长是(     )

    A．21     B．18     C．13     D．15

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    （1）如图（1），在△ABC中，D是BC边上的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．

    ①求证：BE+CF＞EF．

    ②若∠A=90°，探索线段BE、CF、EF之间的数量关系，并加以证明；

    （2）如图（2），在四边形ABCD中，∠B+∠C=180°，DB=DC，∠BDC=120°，以D为顶点作一个60°角，角的两边分别交AB、AC于E、F两点，连接EF，探索线段BE、CF、EF之间的数量关系，并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


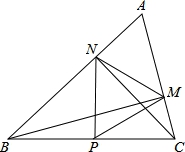
    如图，在△ABC中∠A=60°，BM⊥AC于点M，CN⊥AB于点N，P为BC边的中点，连接PM，PN，则下列结论：①PM=PN；②△PMN为等边三角形；下面判断正确是(     )

    A．①正确     B．②正确     C．①②都正确     D．①②都不正确

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    △ABC中，点O是△ABC内一点且到△ABC三边的距离相等，∠A=40°，则∠BOC=__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


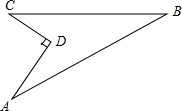
    如图，某住宅小区在施工过程中留下了一块空地，已知AD=8米，CD=6米，∠ADC=90°，AB=26米，BC=24米，小区为美化环境，欲在空地上铺草坪，已知草坪每平方米100元，试问用该草坪铺满这块空地共需花费多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，已知△ABC中，AB=AC，AB边上的垂直平分线DE交AC于点E，D为垂足，若∠ABE：∠EBC=2：1，则∠A=__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    用四舍五入法，把1890mL（精确到1000mL） 取近似值万，用科学记数法可表示为__________mL．

    查看答案和解析>>

    同步练习册答案