
【题目】如图1,将![]() 以点A为中心,逆时针旋转
以点A为中心,逆时针旋转![]() 得到
得到![]() .
.
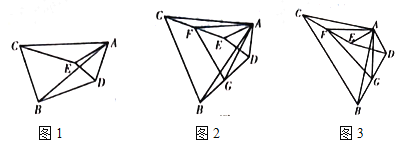
(1)若![]() ,求
,求![]() 的度数:
的度数:
(2)当![]() 时,如图2,点F、G分别是CE、BD的中点,证明:
时,如图2,点F、G分别是CE、BD的中点,证明:![]() 是等边三角形;
是等边三角形;
(3)当![]() 时,如图3,点F、G分别是CE、BD的中点,直接判断
时,如图3,点F、G分别是CE、BD的中点,直接判断![]() 的形状,不需要说明理由.
的形状,不需要说明理由.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() 是等腰直角三角形.
是等腰直角三角形.
【解析】
(1)根据旋转的性质即得![]() ,
,![]() ,进一步即得
,进一步即得![]() ,然后在△ADE中根据三角形的内角和定理求解即可;
,然后在△ADE中根据三角形的内角和定理求解即可;
(2)由旋转的性质可得![]() ,于是有
,于是有![]() ,
,![]() ,
,![]() ,再根据点F、G分别是CE、BD的中点,可得
,再根据点F、G分别是CE、BD的中点,可得![]() ,然后利用SAS可推出
,然后利用SAS可推出![]() ,进而得AF=AG,∠FAE=∠GAD,进一步即得∠FAG=60°,问题即得解决;
,进而得AF=AG,∠FAE=∠GAD,进一步即得∠FAG=60°,问题即得解决;
(3)仿(2)的思路可证得:AF=AG,∠FAG=∠EAD=90°,进而可对△AFG的形状作出判断.
解:(1)由旋转的性质,可得:![]() ,
,![]() .
.
![]() ,即
,即![]() .
.
![]() .
.
(2)证明:由旋转的性质易知![]() .
.
![]() ,
,![]() ,
,![]() .
.
又![]() 点F、G分别是CE、BD的中点,
点F、G分别是CE、BD的中点,
∴![]() ,
,![]() .
.
![]() .
.
∴AF=AG,∠FAE=∠GAD,
![]()
![]()
![]() .
.
![]() 是等边三角形.
是等边三角形.
(3)证明:由旋转的性质易知![]() .
.
![]() ,
,![]() ,
,![]() .
.
又![]() 点F、G分别是CE、BD的中点,
点F、G分别是CE、BD的中点,
∴![]() ,
,![]() .
.
![]() .
.
∴AF=AG,∠FAE=∠GAD,
![]()
![]()
![]() .
.
![]() 是等腰直角三角形.
是等腰直角三角形.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】正比例函数y=x的图象与反比例函数y=![]() 的图象有一个交点的纵坐标是﹣2.
的图象有一个交点的纵坐标是﹣2.
(1)当x=3时,求反比例函数y=![]() 的值;
的值;
(2)当﹣3<x<﹣1时,求反比例函数y=![]() 的取值范围;
的取值范围;
(3)请直接写出关于x的不等式x<![]() <0的解集.
<0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B'在此反比例函数的图象上,则t的值是( )
(x<0)的图象经过点A(﹣2,2),过点A作AB⊥y轴,垂足为B,在y轴的正半轴上取一点P(0,t),过点P作直线OA的垂线l,以直线l为对称轴,点B经轴对称变换得到的点B'在此反比例函数的图象上,则t的值是( )
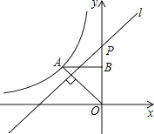
A. 1+![]() B. 4+
B. 4+![]() C. 4
C. 4![]() D. -1+
D. -1+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的![]() 月
月![]() 日为世界环保日,为了提倡低碳环保,某公司决定购买
日为世界环保日,为了提倡低碳环保,某公司决定购买![]() 台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买
台节省能源的新设备,现有甲、乙两种型号的设备可供选购.经调查:购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备多花
台乙型设备多花![]() 万元,购买
万元,购买![]() 台甲型设备比购买
台甲型设备比购买![]() 台乙型设备少花
台乙型设备少花![]() 万元.
万元.
(1)求甲、乙两种型号设备每台的价格;
(2)该公司经决定购买甲型设备不少于![]() 台,预算购买节省能源的新设备资金不超过
台,预算购买节省能源的新设备资金不超过![]() 万元,你认为该公司有哪几种购买方案;
万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备每月的产量为![]() 吨,乙型设备每月的产量为
吨,乙型设备每月的产量为![]() 吨.若每月要求产量不低于
吨.若每月要求产量不低于![]() 吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日是第二十四个“世界读书日“.某校组织读书征文比赛活动,评选出一、二、三等奖若干名,并绘成如图所示的条形统计图和扇形统计图(不完整),请你根据图中信息解答下列问题:

(1)求本次比赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)学校从甲、乙、丙、丁4位一等奖获得者中随机抽取2人参加“世界读书日”宣传活动,请用列表法或画树状图的方法,求出恰好抽到甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】聊城流传着一首家喻户晓的民谣:“东昌府,有三宝,铁塔、古楼、玉皇皋.”被人们誉为三宝之一的铁塔,初建年代在北宋早期,是本市现存最古老的建筑.如图,测绘师在离铁塔10米处的点C测得塔顶A的仰角为α,他又在离铁塔25米处的点D测得塔顶A的仰角为β,若tanαtanβ=1,点D,C,B在同一条直线上,那么测绘师测得铁塔的高度约为(参考数据: ![]() ≈3.162)( )
≈3.162)( )

A. 15.81米 B. 16.81米 C. 30.62米 D. 31.62米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AD=4,E在AB上且AB=4BE,连接CE,作BF⊥CE于F,正方形对角线交于O点,连接OF,将△COF沿CE翻折得△CGF,连接BG,则BG的长为_____.
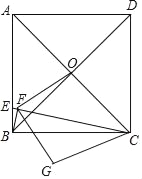
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】己知反比例函数![]() (
(![]() 常数,
常数,![]() ).
).
(1)若点![]()
![]() 在这个函数的图象上,求
在这个函数的图象上,求![]() 的值;
的值;
(2)若在这个函数图象的每一个分支上,![]() 随
随![]() 的增大而增大,求
的增大而增大,求![]() 的取值范围;
的取值范围;
(3)若![]() ,试判断点
,试判断点![]()
![]() 是否在这个函数的图象上,并说明理由.
是否在这个函数的图象上,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com