
| 1 |
| 2 |
| nπR |
| 180 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
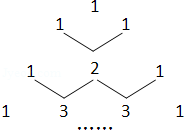 如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数.例如,(a+b)2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字;再如,(a+b)3=a3+3a2b+3ab2+b3展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出(a+b)4的展开式,(a+b)4=
如图是我国古代数学家杨辉最早发现的,称为“杨辉三角”.它的发现比西方要早五百年左右,由此可见我国古代数学的成就是非常值得中华民族自豪的!“杨辉三角”中有许多规律,如它的每一行的数字正好对应了(a+b)n(n为非负整数)的展开式中a按次数从大到小排列的项的系数.例如,(a+b)2=a2+2ab+b2展开式中的系数1、2、1恰好对应图中第三行的数字;再如,(a+b)3=a3+3a2b+3ab2+b3展开式中的系数1、3、3、1恰好对应图中第四行的数字.请认真观察此图,写出(a+b)4的展开式,(a+b)4=查看答案和解析>>
科目:初中数学 来源: 题型:
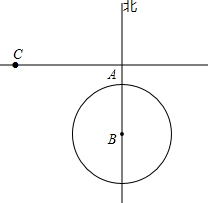 如图,一轮船以40km/h的速度由西向东航行,在途中点C处接到台风警报,台风中心点B正以20km/h的速度由南向北移动.已知距台风中心200km的区域(包括边界)都属于受台风影响区.当轮船接到台风警报时,测得BC=500km,BA=300km.(假定轮船不改变航向).
如图,一轮船以40km/h的速度由西向东航行,在途中点C处接到台风警报,台风中心点B正以20km/h的速度由南向北移动.已知距台风中心200km的区域(包括边界)都属于受台风影响区.当轮船接到台风警报时,测得BC=500km,BA=300km.(假定轮船不改变航向).查看答案和解析>>
科目:初中数学 来源: 题型:
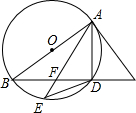 如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.
如图,AB是⊙O的直径,AC是⊙O的切线,BC与⊙O相交于点D,点E在⊙O上,且DE=DA,AE与BC相交于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com