
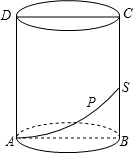
 如图,圆柱的轴截面ABCD,是边长为4的正方形,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离是2$\sqrt{1+{π}^{2}}$.
如图,圆柱的轴截面ABCD,是边长为4的正方形,动点P从A点出发,沿着圆柱的侧面移动到BC的中点S的最短距离是2$\sqrt{1+{π}^{2}}$.  名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.请判断沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;(精确到0.01)
中国“蛟龙”号深潜器目前最大深潜极限为7062.68米.某天该深潜器在海面下1800米处作业(如图),测得正前方海底沉船C的俯角为45°,该深潜器在同一深度向正前方直线航行2000米到B点,此时测得海底沉船C的俯角为60°.请判断沉船C是否在“蛟龙”号深潜极限范围内?并说明理由;(精确到0.01)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 16 | B. | 18 | C. | 20 | D. | 22 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com