
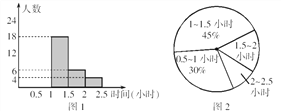
【题目】为了减轻学生的作业负担,教育局规定:初中学段学生每晚的作业总量不超过1.5小时,九(1)班学习委员亮亮对本班每位同学晚上完成作业的时间进行了一次统计,并根据收集的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息,解答下面的问题:
(1)该班共有多少名学生?将图1的条形图补充完整;
(2)计算出作业完成时间在1.5~2小时的部分对应的扇形圆心角;
(3)如果九年级共有500名学生,请估计九年级学生完成作业时间超过1.5小时的有多少人?
科目:初中数学 来源: 题型:
【题目】阅读下列材料: 某种型号的温控水箱的工作过程是:接通电源后,在初始温度20℃下加热水箱中的水;当水温达到设定温度80℃时,加热停止;此后水箱中的水温开始逐渐下降,当下降到20℃时,再次自动加热水箱中的水至80℃时,加热停止;当水箱中的水温下降到20℃时,再次自动加热,…,按照以上方式不断循环.
小明根据学习函数的经验,对该型号温控水箱中的水温随时间变化的规律进行了探究.发现水温y是时间x的函数,其中y(单位:℃)表示水箱中水的温度.x(单位:min)表示接通电源后的时间.
下面是小明的探究过程,请补充完整:
(1)下表记录了32min内14个时间点的温控水箱中水的温度y随时间x的变化情况
接通电源后的时间x | 0 | 1 | 2 | 3 | 4 | 5 | 8 | 10 | 16 | 18 | 20 | 21 | 24 | 32 | … |
水箱中水的温度y | 20 | 35 | 50 | 65 | 80 | 64 | 40 | 32 | 20 | m | 80 | 64 | 40 | 20 | … |
m的值为;
(2)①当0≤x≤4时,写出一个符合表中数据的函数解析式; 当4<x≤16时,写出一个符合表中数据的函数解析式;
②如图,在平面直角坐标系xOy中,描出了上表中部分数据对应的点,根据描出的点,画出当0≤x≤32时,温度y随时间x变化的函数图象:
(3)如果水温y随时间x的变化规律不变,预测水温第8次达到40℃时,距离接通电源min. 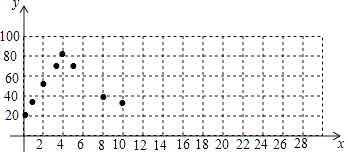
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“C运算”:①当n为奇数时,结果为3n+1;②当n为偶数时,结果为![]() (其中k是使
(其中k是使![]() 为奇数的正整数),并且运算重复进行.例如,n=66时,其“C运算”如下
为奇数的正整数),并且运算重复进行.例如,n=66时,其“C运算”如下
![]()
若n=26,则第2019次“C运算”的结果是
A. 40 B. 5 C. 4 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( ) 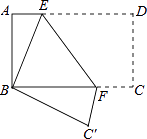
A.3
B.4
C.6
D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
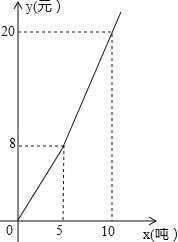
【题目】随着地球上的水资源日益枯竭,各级政府越来越重视节约用水.某市民生活用水按“阶梯水价”方式进行收费,人均月生活用水收费标准如图所示,图中 x 表示人均月生活用水的吨数,y 表示收取的人均月生活用水费(元).请根据图象信息,回答下列问题:
(1)该市人均月生活用水的收费标准是:不超过 5 吨,每吨按 元收取; 超过 5 吨的部分,每吨按 元收取;
(2)当 x>5 时,求 y 与 x 的函数关系式;
(3)若某个家庭有 5 人,五月份的生活用水费共 76 元,则该家庭这个月用了多少吨生活用水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知l1⊥l2 , ⊙O与l1 , l2都相切,⊙O的半径为2cm.矩形ABCD的边AD,AB分别与l1 , l2重合,AB=4 ![]() cm,AD=4cm.若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s).
cm,AD=4cm.若⊙O与矩形ABCD沿l1同时向右移动,⊙O的移动速度为3cm/s,矩形ABCD的移动速度为4cm/s,设移动时间为t(s). 
(1)如图②,两个图形移动一段时间后,⊙O到达⊙O1的位置,矩形ABCD到达A1B1C1D1的位置,此时点O1 , A1 , C1恰好在同一直线上,则移动时间t= .
(2)在移动过程中,圆心O到矩形对角线AC所在直线的距离在不断变化,设该距离为d(cm).当d<2时,求t的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正比例函数y=kx经过点A(2,4),AB⊥x轴于点B. 
(1)求该正比例函数的解析式;
(2)将△ABO绕点A逆时针旋转90°得到△ADC,求点C的坐标;
(3)试判断点C是否在直线y= ![]() x+1的图象上,说明你的理由.
x+1的图象上,说明你的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com