
【题目】如图,正比例函数y=kx经过点A(2,4),AB⊥x轴于点B. 
(1)求该正比例函数的解析式;
(2)将△ABO绕点A逆时针旋转90°得到△ADC,求点C的坐标;
(3)试判断点C是否在直线y= ![]() x+1的图象上,说明你的理由.
x+1的图象上,说明你的理由.
【答案】
(1)解:∵正比例函数y=kx经过点A(2,4),
∴2k=4,解得k=2,
∴该正比例函数的解析式为y=2x
(2)解:∵AB⊥x轴于点B,且A(2,4),
∴OB=2,AB=4.
∵将△ABO绕点A逆时针旋转90°得到△ADC,
∴AD=AB=4,DC=OB=2,
∴D点横坐标为6,C点纵坐标是2,
∴点C的坐标为(6,2)
(3)解:把点C的坐标(6,2)代入y= ![]() x+1,
x+1,
得左边=2,右边= ![]() ×6+1=3,
×6+1=3,
左边≠右边,
即点C不在直线y= ![]() x+1的图象上
x+1的图象上
【解析】(1)将点A(2,4)代入y=kx,利用待定系数法即可求出该正比例函数的解析式;(2)先由AB⊥x轴于点B,且A(2,4),得出OB=2,AB=4.再根据旋转的性质得出AD=AB=4,DC=OB=2,即D点横坐标为6,C点纵坐标是2,进而求出点C的坐标;(3)把点C的坐标(6,2)代入y= ![]() x+1,即可判断.
x+1,即可判断.


科目:初中数学 来源: 题型:
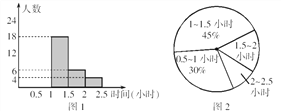
【题目】为了减轻学生的作业负担,教育局规定:初中学段学生每晚的作业总量不超过1.5小时,九(1)班学习委员亮亮对本班每位同学晚上完成作业的时间进行了一次统计,并根据收集的数据绘制了下面两幅不完整的统计图,请你根据图中提供的信息,解答下面的问题:
(1)该班共有多少名学生?将图1的条形图补充完整;
(2)计算出作业完成时间在1.5~2小时的部分对应的扇形圆心角;
(3)如果九年级共有500名学生,请估计九年级学生完成作业时间超过1.5小时的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】服装店10月份以每套500元的进价购进一批羽绒服,当月以标价销售,销售额14000元,进入11月份搞促销活动,每件降价50元,这样销售额比10月份增加了5500元,售出的件数是10月份的1.5倍.
(1)求每件羽绒服的标价是多少元;
(2)进入12月份,该服装店决定把剩余的羽绒服按10月份标价的八折销售,结果全部卖掉,而且这批羽绒服总获利不少于12700元,问这批羽绒服至少购进多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校组织的游艺晚会上,掷飞标游艺区游戏区规则如下,如图掷到A区和B区的得分不同,A区为小圆内部分,B区为大圆内小圆外部分(掷中一次记一个点)现统计小华、小明和小芳掷中与得分情况,如图所示,依此方法计算小芳的得分为( )

A. 76 B. 74 C. 72 D. 70
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
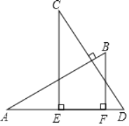
A. a+cB. b+cC. a﹣b+cD. a+b﹣c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△CDE都是等边三角形,B,C,D在一条直线上,连结B,E两点交AC于点M,连结A,D两点交CE于N点.
(1)AD与BE有什么数量关系,并证明你的结论.
(2)求证:CO平分∠BOD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】饺子(如图1)源于古代的角子,饺子原名“娇耳”,相传是我国医圣张仲景首先发明的,距今已有一千八百多年的历史了.有一句民谣叫“大寒小寒,吃饺子过年.”包饺子时,将面团揉成长条状,后用刀切或用手揪成一个个小面团,这些小面团就是箕(jì)子(如图2).擀皮时,将箕子压扁后擀成圆形面皮,一个面箕子可以擀出一个饺子皮(如图3),就可以用来包饺子了.

中国北方,尤其是在京、津地区流行的一种面食﹣合子(如图4),含有团团圆圆的美好寓意.用两层饺子皮在中间加一层馅,就可以包成一个合子.北方有风俗曰:初一的饺子、初二的面、初三的合子往家转.
小亮的妈妈喜爱研究中华美食,自己动手经常给家人做出色香味俱佳的食品.妈妈在传承古人的做法的同时,也进行了加工创新.在每次包饺子临近结束时,如果饺子馅少了,饺子皮多了,这时妈妈会停止包饺子,改包合子,这样既不浪费食材,家人既吃到了饺子又吃到了合子.
这天,妈妈从厨房走到书房,对正在学习的小亮说:“妈妈刚才在厨房包饺子,结果面和多了,做了88个饺子箕,最后包了饺子和合子一共是81个.”
小亮说:“妈妈,我能用刚刚学到的列一元一次方程解应用题的知识和方法得出您包的饺子和合子分别是多少.”
请你写出小亮同学的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,D为⊙O上一点,过 ![]() 上一点T作⊙O的切线TC,且TC⊥AD于点C.
上一点T作⊙O的切线TC,且TC⊥AD于点C. 
(1)若∠DAB=50°,求∠ATC的度数;
(2)若⊙O半径为2,CT= ![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O在边AC上,⊙O与△ABC的边BC,AB分别相切于C,D两点,与边AC交于E点,弦CF与AB平行,与DO的延长线交于M点. 
(1)求证:点M是CF的中点;
(2)若E是 ![]() 的中点,BC=a,写出求AE长的思路.
的中点,BC=a,写出求AE长的思路.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com