
【题目】如图,平面内的直线有相交和平行两种位置关系

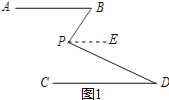
(1)如图①,已知AB∥CD,求证:∠BPD=∠B+∠D;(提示;可过点P作PO∥AB)
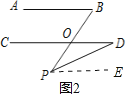
(2)如图②,已知AB∥CD,求证:∠B=∠P+∠D.
【答案】(1)见解析;(2)见解析
【解析】
(1)过点P作PE∥AB,由平行线的性质“两直线平行,内错角相等”得出∠B=∠BPE、∠D=∠DPE,结合角之间的关系即可得出结论;
(2)过点P作PE∥CD,根据平行线的性质即可得出∠B=∠BOD,根据平行线的性质即可得出∠BOD=∠BPE、∠D=∠DPE,结合角之间的关系即可得出结论.
(1)过点P作PE∥AB,如图1所示.
∵AB∥PE,AB∥CD,
AB∥PE∥CD.
∴∠B=∠BPE,∠D=∠DPE
∴∠BPD=∠BPE+∠DPE=∠B+∠D.
(2)过点P作PE∥CD,如图2所示.
∵AB∥CD,
∴∠B=∠BOD,
∵PE∥CD,
∴∠BOD=∠BPE;∠D=∠DPE
∴∠BPE=∠BPD+∠DPE=∠BPD+∠D
∴∠BOD=∠BPD +∠D
即∠B=∠BPD +∠D.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:
【题目】如图所示,已知∠AOB和一条定长线段a,在∠AOB内找一点P,使点P到OA,OB的距离都等于a,作法如下:
①在∠AOB内作OB的垂线段NH,使NH=a,H为垂足;②过N作NM∥OB;③作∠AOB的平分线OP,与NM交于点P;④点P即为所求.其中③的依据是( )

A. 平行线之间的距离处处相等 B. 角的内部到角的两边的距离相等的点在角的平分线上
C. 角的平分线上的点到角的两边的距离相等 D. 线段垂直平分线上的点到线段两端点的距离相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,![]() ,
,![]() cm,
cm,![]() cm,若以C为圆心,以2cm为半径作圆,则点A在⊙C_____;点B在⊙C________;若以AB为直径作⊙O,则点C在⊙O_______.
cm,若以C为圆心,以2cm为半径作圆,则点A在⊙C_____;点B在⊙C________;若以AB为直径作⊙O,则点C在⊙O_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一蓄水池有水40m3,按一定的速度放水,水池里的水量y(m3)与放水时间t(分)有如下关系:
放水时间(分) | 1 | 2 | 3 | 4 | … |
水池中水量(m3) | 38 | 36 | 34 | 32 | … |
下列结论中正确的是( )
A. y随t的增加而增大
B. 放水时间为15分钟时,水池中水量为8m3
C. 每分钟的放水量是2m3
D. y与t之间的关系式为y=40t
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在小正方形组成的的网格纸中,四边形ABCD和四边形A2B2C2D2的位置如图所示.

(1)现把四边形ABCD绕C点按顺时针方向旋转90°,画出相应的图形A1B1C1D1,
(2)若四边形A1B1C1D1平移后,与四边形A2B2C2D2成轴对称,写出满足要求的一种平移方法,并画出平移后的图形A3B3C3D3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与直线
的图象与直线![]() 交于点A(3,m).
交于点A(3,m).
(1)求k、m的值;
(2)已知点P(n,n)(n>0),过点P作平行于![]() 轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数
轴的直线,交直线y=x-2于点M,过点P作平行于y轴的直线,交函数![]() 的图象于点N.
的图象于点N.
①当n=1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM,结合函数的图象,直接写出n的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,沿EF将矩形折叠,使A、C重合,AC与EF交于点H.
(1)求证:△ABE≌△AGF;
(2)若AB=6,BC=8,求△ABE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图,反比例函数![]() 的图象经过点A(1,4),直线y=2x+b(b≠0)与双曲线
的图象经过点A(1,4),直线y=2x+b(b≠0)与双曲线![]() 在第一、三象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.(1)求k的值;(2)当b=-3时,求△OCD的面积;
在第一、三象限分别相交于P,Q两点,与x轴、y轴分别相交于C,D两点.(1)求k的值;(2)当b=-3时,求△OCD的面积;
(3)连接OQ,是否存在实数b,使得S△ODQ=S△OCD?若存在,请求出b的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,点
,点![]() 在第一象限,
在第一象限,![]() 为等边三角形,
为等边三角形,![]()
![]() ,垂足为点
,垂足为点![]() .
.![]()
![]() ,垂足为
,垂足为![]() .
.

(1)求OF的长;
(2)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连
,连![]() 交
交![]() 于E,求OE的长.
于E,求OE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com