
【题目】在平行四边形ABCD中,点E是AD边上一点,连接CE,交对角线BD于点F,过点A作AB的垂线交BD的延长线于点G,过B作BH垂直于CE,垂足为点H,交CD于点P,2∠1+∠2=90°.
(1)若PH=2,BH=4,求PC的长;
(2)若BC=FC,求证:GF=![]() PC.
PC.

【答案】(1)2![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)根据四边形ABCD是平行四边形,先证∠BCP=∠BPC,再根据勾股定理即可求出答案;
(2)由(1)得:BC=BP=AD,可知四边形ABPD是等腰梯形,从而证∠1=∠GAD,然后证△DAG≌△FCD,作FM⊥CD于M,BN⊥CD于N,△CFM≌△BPN即可求出答案.
(1)解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,AB∥CD,AB=CD,
∴∠BCH=∠2,
∴∠BCP=∠2+∠1,
∵2∠1+∠2=90°.
∴∠BCP=90°﹣∠1,
∵BH⊥CE,
∴∠BPC+∠1=90°,
∴∠BPC=90°﹣∠1,
∴∠BCP=∠BPC,
∴BC=BP=BH+PH=4+2=6,
∴CH2=BC2﹣BH2=62﹣42=20,
∴PC=![]() =
=![]() =2
=2![]() ;
;
(2)证明:由(1)得:BC=BP=AD,
∴四边形ABPD是等腰梯形,
∴∠DAB=∠PBA,
∵CD∥AB,
∴∠PBA=∠BPC,
∵BH⊥CE,
∴∠1=90°﹣∠BPC=90°﹣∠PBA=90°﹣∠DAB=∠GAD,
∵AD=BC,BC=FC,
∴AD=FC,∠CBF=∠CFB,
∵AD∥BC,
∴∠EDF=∠CBF,
∴∠EDF=∠CFB=∠EFD,
∴∠ADG=∠CFD,
在△DAG和△FCD中,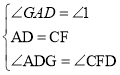 ,
,
∴△DAG≌△FCD(ASA),
∴AG=CD=AB,DG=FD,
∵AG⊥AB,
∴△ABG是等腰直角三角形,
∴∠DBA=∠G=45°,
作FM⊥CD于M,BN⊥CD于N,如图所示:
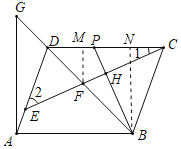
∵AB∥CD,
∴∠CDF=∠DBA=45°,
∴△DMF是等腰直角三角形,
∴DM=FM,DF=![]() FM,
FM,
∵BN⊥CD,BH⊥CE,
∴由三角形内角和定理得:∠1=∠PBN,
在△CFM和△BPN中,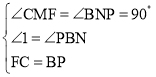 ,
,
∴△CFM≌△BPN(AAS),
∴FM=PN,
∵BC=BP,BN⊥CD,
∴PN=CN,
∴PC=2PN=2FM=![]() DF,
DF,
∴![]() PC=2DF,
PC=2DF,
∴GF=2DF=![]() PC
PC


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
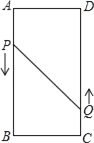
【题目】如图,A、B、C、D为矩形的4个顶点,AB=16cm,BC=6cm,动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发,点Q从点C向点D移动.
(1)若点P从点A移动到点B停止,点P、Q分别从点A、C同时出发,问经过2s时P、Q两点之间的距离是多少cm?
(2)若点P从点A移动到点B停止,点Q随点P的停止而停止移动,点P、Q分别从点A、C同时出发,问经过多长时间P、Q两点之间的距离是10cm?
(3)若点P沿着AB→BC→CD移动,点P、Q分别从点A、C同时出发,点Q从点C移动到点D停止时,点P随点Q的停止而停止移动,试探求经过多长时间△PBQ的面积为12cm2?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图①,在![]() 中
中![]() ,
,![]() ,
,![]() 是过
是过![]() 的一条直线,且
的一条直线,且![]() ,
,![]() 在
在![]() 的异侧,
的异侧,![]() 于
于![]() ,
,![]() 于
于![]() .
.
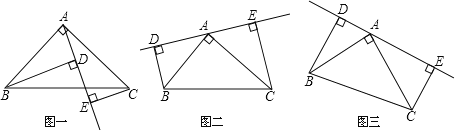
(1)填空:线段![]() 与
与![]() 、
、![]() 之间的数量关系为________;
之间的数量关系为________;
(2)若直线![]() 绕
绕![]() 点旋转到如图②位置时(
点旋转到如图②位置时(![]() ),其他条件不变,判断
),其他条件不变,判断![]() 与
与![]() ,
,![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)若直线![]() 绕
绕![]() 点旋转到如图③位置时(
点旋转到如图③位置时(![]() ),其他条件不变,则
),其他条件不变,则![]() 与
与![]() ,
,![]() 的关系又怎样?请写出结果,不必证明.
的关系又怎样?请写出结果,不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图像与直线
的图像与直线![]() 交于点
交于点![]() 、点
、点![]() .
.
(1)求![]() 的表达式和
的表达式和![]() 的值;
的值;
(2)当![]() 时,求自变量
时,求自变量![]() 的取值范围;
的取值范围;
(3)将直线![]() 沿
沿![]() 轴上下平移,当平移后的直线与抛物线只有一个公共点时,求平移后的直线表达式.
轴上下平移,当平移后的直线与抛物线只有一个公共点时,求平移后的直线表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
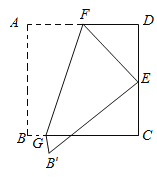
【题目】如图,将边长为4的正方形纸片ABCD折叠,使得点A落在边CD的中点E处,折痕为FG,点F、G分别在边AD、BC上,则折痕FG的长度为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,点P是△ABD的内切圆的圆心,过P作PE⊥BC,PF⊥CD,垂足分别为点E、F,则四边形PECF和矩形ABCD的面积之比等于( )

A.1:2B.2:3C.3:4D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
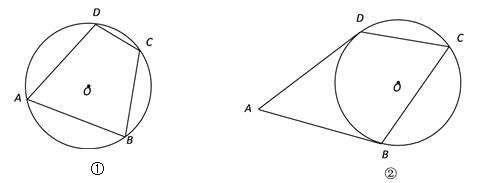
【题目】已知⊙O,请用无刻度的直尺完成下列作图.
(1)如图①,四边形ABCD是⊙O的内接四边形,且AB=AD,画出∠BCD的角平分线;
(2)如图②,AB和AD是⊙O的切线,切点分别是B、D,点C在⊙O上,画出∠BCD的角平分线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直角坐标平面上的ΔABC,AC=CB,∠ACB=90°,且A(-1,0),B(m,n),C(3,0).若抛物线![]() 经过A、C两点.
经过A、C两点.
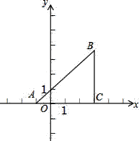
(1)求a、b的值;
(2)将抛物线向上平移若干个单位得到的新抛物线恰好经过点B,求新抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC 是等边三角形,D 为 CB 延长线上一点,E 为 BC 延长线上点.
(1)当 BD、BC 和 CE 满足什么条件时,△ADB∽△EAC?
(2)当△ADB∽△EAC 时,求∠DAE 的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com