
如图1,在平面直角坐标系中,二次函数y=ax2 -2x+2的图象与y轴交于点C,以OC为一边向左侧作正方形OCBA,点B刚好落在抛物线上.
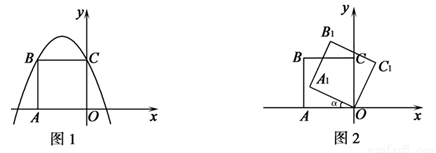
(1)求a的值;
(2)若点D在二次函数y=ax2 -2x+2的图象的对称轴上,点E在二次函数y=ax2 ﹣2x+2的图象上,是否存在以B,C,D,E四点为顶点的四边形为平行四边形?若存在,请直接写出所有满足条件的点E的坐标;若不存在,请说明理由.
(3)如图2,把正方形OCBA绕点O顺时针旋转α后得到正方形A1B1C1O(0°<α<90°)。在旋转过程中,若点A1落在二次函数y=ax2﹣2x+2的图象对称轴上,求出此时的点B1的坐标.
(1)-1;(2)(-1,3)或(-3,-1)或(1,-1),(3)(2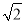 sin15°,2
sin15°,2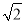 cos15°).
cos15°).
【解析】
试题分析:(1)先求出点C的坐标,再根据正方形的边长相等,得出点B的坐标,代入y=ax2-2x+2,即可得出a的值.
(2)分两种情况求【解析】
①当点E在抛物线顶点时;②当BC∥DE,且DE=BC=2时,即可求出答案;
(3)①由点A1落在二次函数对称轴上,OA1=2,可得出∠A1OA=60°,进而得出∠BOB1=60°,求出∠B1OC=15°,利用三角函数表示点B1的坐标即可;
②设F(-1,m),由△A1B1F∽△HOF得出A1F=2m,由OB1=OB=2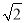 ,得出B1H=
,得出B1H=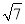 ,在Rt△A1B1F中由勾股定理A1F2+A1B12=B1F2,列出方程(2m)2+22=(
,在Rt△A1B1F中由勾股定理A1F2+A1B12=B1F2,列出方程(2m)2+22=(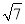 -m)2求出m的值,即可得出点F的坐标.
-m)2求出m的值,即可得出点F的坐标.
试题解析:(1)二次函数y=ax2-2x+2的图象与y轴交于点C,
∴C(0,2),
∵以OC为一边向左侧作正方形OCBA,点B刚好落在抛物线上.
∴B(-2,2),把B(-2,2)代入y=ax2-2x+2,得2=4a+4+2,解得a=-1
(2)①当点E在抛物线顶点时,
∵二次函数的解析式为y=-x2-2x+2.
∴E(-1,3)
∵点D在二次函数的对称轴上,
∴当E(-1,3)以B,C,D,E四点为顶点的四边形为平行四边形
②当BC∥DE,且DE=BC=2时,
∵点D在二次函数的对称轴上,
∴D的横坐标为-1,
∴设点E的横坐标为t,则有-1-t=2,或t-(-1)=2,解得t=-3或1.
∴E(-3,-1)或(1,-1)
综上所述:当点E的坐标为(-1,3)或(-3,-1)或(1,-1),以B,C,D,E四点为顶点的四边形为平行四边形.
(3)如图1,
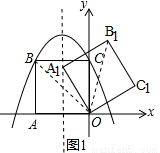
∵点A1落在二次函数对称轴上,OA1=2
∴∠A1OA=60°,
∴∠BOB1=60°,
∴∠B1OC=60°-45°=15°,
∵OB1=OB=2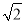 ,
,
∴B1(2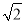 sin15°,2
sin15°,2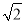 cos15°).
cos15°).
考点:二次函数综合题.


科目:初中数学 来源:2014-2015学年山东省滨州地区九年级12月月考数学试卷(解析版) 题型:选择题
如图,在?ABCD中,E为CD上一点,连接AE、BD,且AE、BD交于点F,S△DEF:S△ABF=4:25,则DE:EC=( )
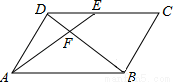
A、2:5 B、2:3 C、3:5 D、3:2
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省吉安市朝宗实验学校九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,这是圆桌正上方的灯泡(看作一个点)发出的光线照射到圆桌后在地面上形成圆形的示意图.已知桌面直径为1.2m,桌面离地面1m. 若灯泡离地面3m,则地面上阴影部分的面积为__________.
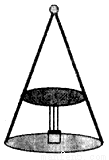
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江西省吉安市朝宗实验学校九年级上学期期中考试数学试卷(解析版) 题型:选择题
在同一平面直角坐标系中,函数y=mx+m与y=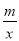 (m≠0)的图象可能是( )
(m≠0)的图象可能是( )
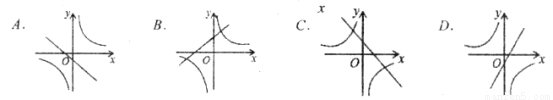
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区西片九年级12月月考数学试卷(解析版) 题型:解答题
二次函数y=ax2+c (a≠0)的图象经过点A(1,-1),B(2,5),
(1)求函数y=ax2+c的表达式。
(2)若点C(-2,m),D(n ,7)也在函数的图象上,求点C的坐标;点D的坐标。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省盐城市盐都区西片九年级12月月考数学试卷(解析版) 题型:填空题
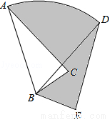
如图,在△ABC中,AB=6,将△ABC绕点B顺时针旋转60°后得到△DBE,点A经过的路径为弧AD,则图中阴影部分的面积是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏盐城东台苏东双语学校九年级上学期第一次检测二数学试卷(解析版) 题型:解答题
(本题满分10分)如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.

(1)当BC=1时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com